Dans cette leçon de géométrie pour les élèves de CM1–CM2, nous allons travailler sur les triangles. Les élèves découvriront qu’un triangle est un polygone qui a trois côtés, trois sommets et trois angles, puis ils apprendront à reconnaître différents triangles particuliers : triangle rectangle (avec un angle droit), triangle isocèle (avec deux côtés de même longueur) et triangle équilatéral (avec trois côtés de même longueur). À partir de figures à trier, de constructions à la règle, au compas et à l’équerre, ils apprendront à identifier, nommer et décrire ces triangles en utilisant un vocabulaire géométrique précis.
Clique ici pour revenir sur la page d’accueil !
Géom 9/10/11 : Les triangles
Géom 9 : Le triangle
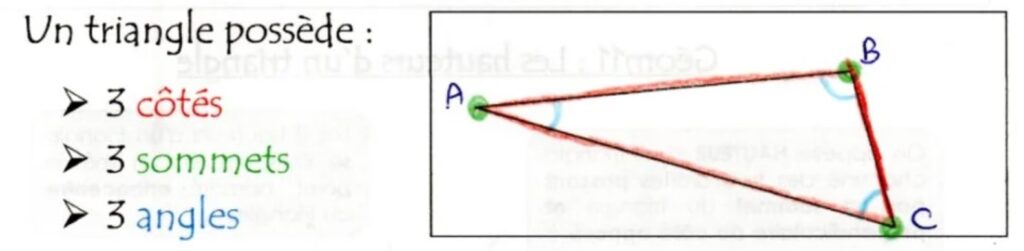
C’est un polygone à 3 côtés et 3 sommets. C’est la figure géométrique la plus simple qui existe.
- 3 côtés : les 3 segments qui le forment
- 3 sommets : les points où se rejoignent les côtés (A, B et C)
- 3 angles formés entre deux côtés
Comment effectuer une classification ?
Il existe quatre types de triangles.
| Type | Description |
|---|---|
| Triangle équilatéral | 3 côtés égaux et 3 angles égaux (60° chacun) |
| Triangle isocèle | 2 côtés égaux et 2 angles égaux |
| Triangle rectangle | 1 angle droit (exactement 90°) – pas de côtés égaux |
| Triangle rectangle isocèle | 1 angle droit (exactement 90°) + 2 côtés égaux |
| Triangle quelconque | 3 côtés de longueurs différentes |
La somme des angles est toujours égale à 180°.
Géom 10 : Comment construire des triangles ?
On trace le segment [AB] de longueur 8 cm, puis un arc de cercle de centre A et de rayon 6 cm, correspondant à la longueur du côté [AC]. Il faut ensuite tracer ensuite un arc de cercle de centre B et de rayon 4 cm, correspondant à la longueur du côté [BC]. Le point d’intersection des deux arcs de cercle est à 6 cm de A et 4 cm de B. C’est le point C. On trace alors le triangle ABC.
Attention, les mesures (longueurs) ne sont pas correctes, il s’agit d’un schéma !
Géom 11 : Les hauteur d’un triangle
On appelle « hauteur » d’un triangle chacune des trois droites passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet. Les trois hauteurs d’un triangle se coupent en même point nommé orthocentre du triangle. Le point d’intersection d’une hauteur et d’un côté s’appelle le pied de la hauteur.
Quelles compétences travaille-t-on autour des triangles ?
| Compétence | Indicateur de réussite | Lien vers une ressource |
|---|---|---|
| Comprendre les triangles | L’élève sait qu’un triangle est un polygone à 3 côtés et 3 angles. | Leçon Géométrie G10 : Les triangles – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |
| Identifier triangle équilatéral/isocèle | L’élève repère : équilatéral (3 côtés égaux) ; isocèle (2 côtés égaux). | Triangles CM1/CM2 – SOS Cartables ; Géométrie CM2 – SOS Cartables. |
| Classer par côtés et angles | L’élève identifie : scalène (3 côtés différents) ; rectangle (1 angle droit). | Leçon Géométrie G10 : Les triangles – SOS Cartables ; Programme cycle 3 – Éduscol. |
| Reproduire triangles simples | L’élève trace : triangle équilatéral, rectangle avec règle/équerre. | Reproduction triangles – SOS Cartables ; Mathématiques CM2 – SOS Cartables. |
| Calculer périmètres triangles | L’élève calcule : 3+4+5=12 cm ; équilatéral 4×3=12 cm. | Exercices triangles Série 1 – SOS Cartables ; Triangles CM2 – SOS Cartables. |
| Identifier propriétés angles | L’élève vérifie : somme angles = 180° ; triangle rectangle (angle droit). | Triangles – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |