En numération, les élèves de CM1 et de CM2 passent d’un simple maniement des nombres à une véritable compréhension de notre système de numération décimale : grands nombres entiers, nombres décimaux, changements d’unités, décompositions, comparaisons et écritures diverses. Dans cet article, je regroupe toutes mes leçons de numération pour le double niveau CM1‑CM2, afin de proposer une progression claire, cohérente et clé en main, du rappel des bases jusqu’aux notions plus complexes.
Vous y trouverez des traces écrites prêtes à l’emploi, pour mieux comprendre et à manipuler les nombres au quotidien, en classe comme en autonomie. Tu peux revenir sur la page d’accueil en cliquant ici !
Leçons de numération N1 Les nombres entiers < 1 000 000
Lire et écrire les nombres entiers
Lorsque tu écris un nombre en chiffres, il faut laisser un espace entre les classes pour faciliter la lecture du nombre. Ici nous allons analyser le nombre 524 671.

524 671 se lit cinq-cent-vingt-quatre-mille-six-cent-soixante-et-onze.
Chiffres et nombres
524 671
2 est le chiffre des dizaines de mille. 6 est le chiffre des centaines d’unités simples
52 est le nombre des dizaines de milliers. 524 est le nombre d’unités de mille
Décomposer les nombres entiers :
Décomposition additive :
Exemple : 416 725 = 400 000 + 10 000 + 6 000 + 700 + 20 + 5
La décomposition multiplicative avec parenthèses :
Exemple : 416 725 = (4 x 100 000) + (1 x 10 000) + (6 x 1 000) + (7 x 100) + (2 x 10) + (5 x 1)
Comparer les nombres entiers
Si deux nombres entiers n’ont pas le même nombre de chiffres, le nombre le plus grand est celui qui a le plus de chiffres.
Si deux nombres entiers ont le même nombre de chiffres, on compare les chiffres un à un de gauche à droite.
Exemples : 9 453 > 8 914 car 9 > 8 8 453 < 8 914 car 4 < 9
Ranger les nombres entiers
Ranger dans l’ordre croissant, c’est ranger du plus petit au plus grand ! 0 < 1 < 2
Exemple : 1 000 < 525 000 < 650 200 < 750 980
Ranger dans l’ordre décroissant, c’est ranger du plus grand au plus petit ! 2 > 1 > 0
Exemple : 750 980 > 650 200 > 525 000 > 1 000
Encadrer les nombres entier
On peut encadrer à la dizaine près : 252 363 (exemple complexe)
Dans un premier temps, on recherche le chiffre des dizaines : 252 363. Ensuite, on trouve le nombre de dizaines : 252 363. Il s’agit du nombre de paquets de 10 que l’on peut faire. On peut faire 25 236 paquets puis on positionne le zéro des unités. –> 252 360 On a ainsi 252 360 < 252 363 < ?
Comme nous encadrons à la dizaine près, on avance donc de 10 en 10. On ajoute alors une dizaine supplémentaire, il y a donc 25 237 paquets. On positionne alors le zéro des unités. –> 252 370
252 360 < 252 363 < 252 370

Leçons de numération N2 Les grands nombres
Lire et écrire les grands nombres
Lorsque tu écris un nombre en chiffres, il faut laisser un espace entre les classes pour faciliter la lecture du nombre. Ici nous allons analyser le nombre 5 246 719.
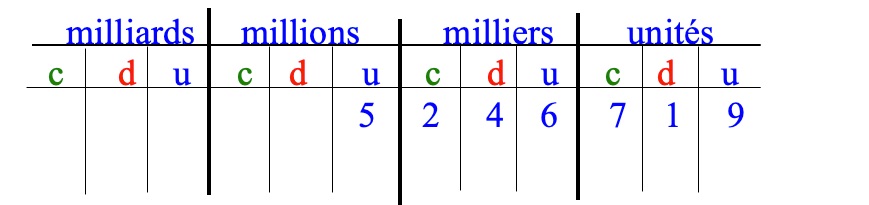
5 246 719 se lit cinq-millions-deux-cent-quarante-six-mille-sept-cent-dix-neuf
Attention ! Mille est invariable
Cent ne prend un « s » seulement lorsqu’il est situé à la fin du nombre. –> Mille-trois-cents
Les grands nombres : chiffres de et nombres de
5 246 719
2 est le chiffre des centaines de mille 6 est le chiffre des unités simples
5 est le chiffre des unités de millions
52 est le nombre des centaines de milliers. 5 246 est le nombre de milliers.
Décomposer les grands nombres :
Décomposition additive :
Exemple : 8 416 725 = 8 000 000 + 400 000 + 10 000 + 6 000 + 700 + 20 + 5
La décomposition multiplicative avec parenthèses :
Exemple : 8 416 725 = (8 x 1 000 000) + (4 x 100 000) + (1 x 10 000) + (6 x 1 000) + (7 x 100) + (2 x 10) + (5 x 1)
Comparer et ranger les grands nombres entiers
Si deux nombres entiers n’ont pas le même nombre de chiffres, le nombre le plus grand est celui qui a le plus de chiffres.
Si deux nombres entiers ont le même nombre de chiffres, on compare les chiffres un à un de gauche à droite.
Exemples : 9 025 453 > 8 025 914 car 9 > 8 8 453 058 < 8 914 058 car 4 < 9
Ranger dans l’ordre croissant, c’est ranger du plus petit au plus grand ! 0 < 1 < 2
Exemple : 1 000 < 525 000 < 650 200 < 750 980 < 1 000 000 < 22 500 800
Ranger dans l’ordre décroissant, c’est ranger du plus grand au plus petit ! 2 > 1 > 0
Exemple : 22 500 800 > 1 000 000 > 750 980 > 650 200 > 525 000 > 1 000
Encadrer et intercaler les grands nombres
On peut encadrer à la dizaine près : 7 252 363 (exemple complexe)
Dans un premier temps, on recherche le chiffre des dizaines : 7 252 363. Ensuite, on trouve le nombre de dizaines : 7 252 363. Il s’agit du nombre de paquets de 10 que l’on peut faire. On peut faire 725 236 paquets puis on positionne le zéro des unités. –> 7 252 360 On a ainsi 7 252 360 < 252 363 < ?
Comme nous encadrons à la dizaine près, on avance donc de 10 en 10. On ajoute alors une dizaine supplémentaire, il y a donc 725 237 paquets. On positionne alors le zéro des unités. –> 7 252 370
7 252 360 < 252 363 < 7 252 370

Intercaler des nombres consiste à placer un ou plusieurs nombres entre deux nombres donnés pour respecter l’ordre croissant. Avec les grands nombres, cela permet de mieux comprendre leur taille et leur position sur la droite numérique. Par exemple, entre 7 000 000 et 7 000 010, on peut intercaler 7 000 001, 7 000 002, 7 000 003… et ainsi de suite. Cette activité aide à comparer, ranger et repérer les nombres très grands. Intercaler des nombres développe aussi la maîtrise des unités, dizaines, centaines, milliers et millions, car il faut observer précisément chaque chiffre pour trouver les nombres intermédiaires corrects. C’est un outil essentiel pour manipuler les grands nombres avec précision.
Leçons de numération N3-N4 Les fractions usuelles
Définition des fractions usuelles.
Une fraction est un nombre qui représente des parts égales de l’unité (par exemple des parts égales de gâteau).
Dans une fraction, il y a 2 nombres :
- un nombre pour dire combien de parts on prend : le numérateur.
- un nombre pour dire en combien de parts on partage l’unité : le dénominateur.
Sens des fractions
On utilise une fraction :
- Pour préciser combien de parts égales on prend dans une ou plusieurs unités. Exemple : Un disque partagé en 6 parts égales, 5 parts colorées.
- Pour désigner un rapport entre deux quantités
Exemple : Dans un bouquet de 15 fleurs, il y a 5 roses.
- Pour repérer des sous-graduations
Lire et écrire les fraction
Quand on partage une unité en parts égales on obtient des fractions de l’unité.
Exemple d’image : une unité partagée en 7 parts égales, 3 parts colorées

- 3 représente le nombre de parts coloriées : c’est le numérateur.
- 7 représente le nombre de parts qui partagent l’unité : c’est le dénominateur.
Pour lire une fraction, on lit d’abord le numérateur puis le dénominateur que l’on fait suivre du suffixe
-ième.

Leçons de numération N5 Les fractions décimales


Leçons de numération N6-N7 Les nombres décimaux
Ecrire les nombres décimaux
Un nombre décimal peut s’écrire sous forme de fraction décimale ou avec une virgule.
| Fraction | Signification | Écriture à virgule | Lecture |
|---|---|---|---|
| 1/10 | 1 : 10 l’unité est divisée en 10 | 0,1 | un dixième |
| 1/100 | 1 : 100 l’unité est divisée en 100 | 0,01 | un centième |
| 1/1 000 | 1 : 1 000 l’unité est divisée en 1 000 | 0,001 | un millième |
| 1/10 000 | 1 : 10 000 l’unité est divisée en 10 000 | 0,0001 | un dix-millième |
Lire les nombres décimaux

La virgule est toujours placée après le chiffre des unités.
| Partie entière | Virgule | Partie décimale |
|---|---|---|
| 15 | , | 628 |
À gauche de la virgule, c’est la partie entière.
À droite de la virgule, c’est la partie décimale.
On peut lire :
- « quinze virgule six-cent-vingt-huit »
- « quinze et six-cent-vingt-huit millièmes »
- « quinze-mille-six-cent-vingt-huit millièmes »
Placer les nombres décimaux dans un tableau
Pour pouvoir écrire les nombres décimaux, il faut rajouter des colonnes à droite du tableau des entiers.
| 10 000 | 1 000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1 000 | 1/10 000 |
|---|---|---|---|---|---|---|---|---|
| dizaines de mille | unités de mille | centaines | dizaines | unités | dixièmes | centièmes | millièmes | dix-millièmes |
| 0 | 0 | 3 | 0 | 5 | 6 | 2 | 0 | 0 |
Ce nombre s’écrit 305,62. On n’écrit pas les zéros à gauche de la partie entière, ni les zéros à droite de la partie décimale.
Décomposer un nombre décimal
- Décomposition : partie entière / partie décimale –> 37,642= 37 + 0,642
- Décomposition additive –> 37,642 = 30 + 7+ 0,6 + 0,04 + 0,002
- Décomposition multiplicative –> 37,642 = (3X10)+ (7×1) + (6X0,1)+(4X0,01)+(2X0,001)
Comparer et ranger des nombres décimaux
Pour comparer deux nombres décimaux, il faut penser à la valeur de chaque chiffre.
Il faut d’abord comparer la partie entière : 12,5<15,6 car 12<15
Si la partie entière est égale alors il faut regarder la partie décimale : 6,3 < 6,4 car 3<4
S’il n’y a pas le même nombre de chiffre au niveau de la partie décimale pour les 2 nombres, on positionne des « 0 » à droite (dans la partie décimale) pour que cela soit le cas.
Ex : 0,34 < 0,4 car 0,34 < 0,40 (en effet 4 dixièmes correspondent à 40 centièmes)
Autre exemple : 1,6>1,321 car 1,600>1,321 car 600 millièmes > 321 millièmes
Encadrer des nombres décimaux
Pour encadrer un nombre décimal entre deux nombres décimaux, on cherche le nombre qui le précède (avant) et le nombre qui le suit (après). On peut encadrer entre deux entiers 5 < 5,64 < 6 ou entre deux dixièmes 5,6 < 5,64 < 5,7
Placer des nombres décimaux sur une droite graduée
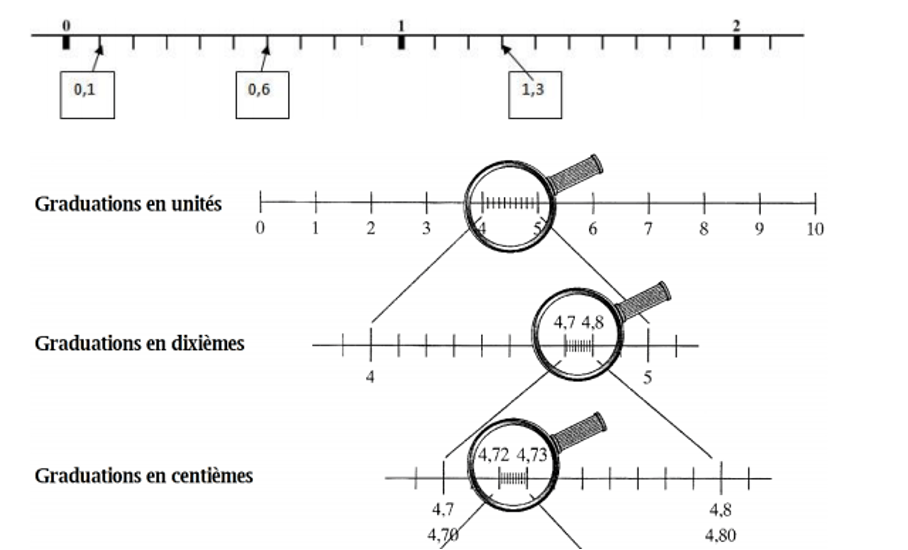
Les nombres décimaux sont un type de nombre utilisé dans les mathématiques pour représenter des valeurs non entières, c’est-à-dire des fractions ou des parties d’un tout.
Dans un premier temps, nous allons définir la notion de « nombre décimal ». On indiquera comment on peut transformer une fraction décimale en un nombre décimal et inversement.
Le groupe classe apprendra à les lire et à les écrire avec des mots importants comme « dizaine », « unité », « dixième », « centième » ou « millième ». On verra qu’il y a plusieurs façons d’écrire un nombre décimal : 5,023
cinq virgule zéro-vingt-trois
cinq unités et vingt-trois millièmes
cinq-mille-vingt-trois millièmes
On travaillera à nouveau la valeur positionnelle des chiffres et le nombre de centaines par exemple.
Le groupe classe apprendra ensuite à décomposer de façon additive et multiplicative des nombres décimaux.
10,602 = 10 + 0,6 + 0,002 = (1×10) + (6×0,1) + (2×0,001)
Par la suite, on pourra comparer et ranger les nombres dans l’ordre croissant ou décroissant. On pourra également les nombres à l’unité près, à la dizaine de mille près, à la centaine de millions près…
L’utilisation des droites graduées est très importante en CM2 pour développer la compréhension des nombres décimaux et leur positionnement précis sur une échelle numérique. Les élèves apprennent à analyser une droite graduée en identifiant l’origine, l’unité, l’échelle et les graduations intermédiaires, puis à replacer des nombres comme 2,3 ; 1,75 ou 4,2 avec exactitude.
| Leçons de numération | Compétence principale CM1–CM2 (formulation élève) : leçons de numération |
|---|---|
| Grands nombres entiers Leçons de numération | Lire, écrire, décomposer et recomposer des grands nombres entiers (jusqu’au moins au million, puis davantage en CM2), en comprenant la valeur de chaque chiffre selon sa place. |
| Numération de position Leçons de numération | Comprendre et utiliser les règles de la numération décimale de position (unités, dizaines, centaines, milliers, etc.) pour comparer, ranger et encadrer des nombres. |
| Comparer / ranger des entiers Leçons de numération | Comparer, ranger et encadrer des grands nombres entiers, les repérer et les placer sur une demi-droite graduée adaptée. |
| Fractions simples Leçons de numération | Reconnaître et utiliser des fractions simples (½, ⅓, ¼, ¾, etc.) pour représenter un partage ou une part d’un tout ; comparer quelques fractions simples. Leçons de numération |
| Fractions décimales Leçons de numération | Comprendre qu’une fraction décimale (1/10, 3/10, 47/100…) correspond à un partage en 10, 100, 1000 parts égales et prépare l’écriture décimale. Leçons de numération |
| Nombres décimaux (écriture) Leçons de numération | Lire, écrire et décomposer des nombres décimaux (dixièmes, centièmes…) sous différentes formes (écriture à virgule, fraction décimale, décomposition en unités + dixièmes + centièmes). |
| Nombres décimaux (repérage) Leçons de numération | Comparer, ranger, encadrer des nombres décimaux et les placer sur une demi-droite graduée ; les relier à des mesures (longueurs, masses, prix…). Leçons de numération |
| Passer d’une écriture à l’autre Leçons de numération | Passer d’une écriture décomposée à l’écriture chiffrée et inversement (ex. 4 000 + 300 + 5 = 4 305 ; 2 unités et 7 dixièmes = 2,7 ; 37/10 = 3,7). Leçons de numération |
| Calcul mental et estimation Leçons de numération | Utiliser la connaissance des nombres pour calculer mentalement (additions, soustractions, multiplications simples, quotients simples) et estimer un ordre de grandeur d’un résultat. |
| Problèmes utilisant entiers, fractions, décimaux Leçons de numération | Résoudre des problèmes en utilisant les grands nombres entiers, les fractions simples et les nombres décimaux, en choisissant une écriture adaptée à la situation. Leçons de numération |

