Manipuler les propriétés des tableaux de proportionnalité (voir leçon)
Approche sur les propriétés du tableau de proportionnalité n°1
Jean veut acheter des oranges. Le prix des oranges est proportionnel à la masse achetée. Il sait que Margot a acheté 3kg d’orange pour 3,90€.
De plus, on sait que Margot a acheté 4kg d’orange pour 5,20€. Jean compte acheter 7 kg d’orange. Combien devra-t-il payer ?
| Quantité | 3 | 4 | 7 |
| Prix | 3.90 | 5.20 | ?????? |
Un tableau de proportionnalité permet de représenter deux grandeurs proportionnelles. Il est constitué de deux lignes (ou colonnes) où chaque valeur de la deuxième ligne est proportionnelle à la valeur correspondante de la première ligne.
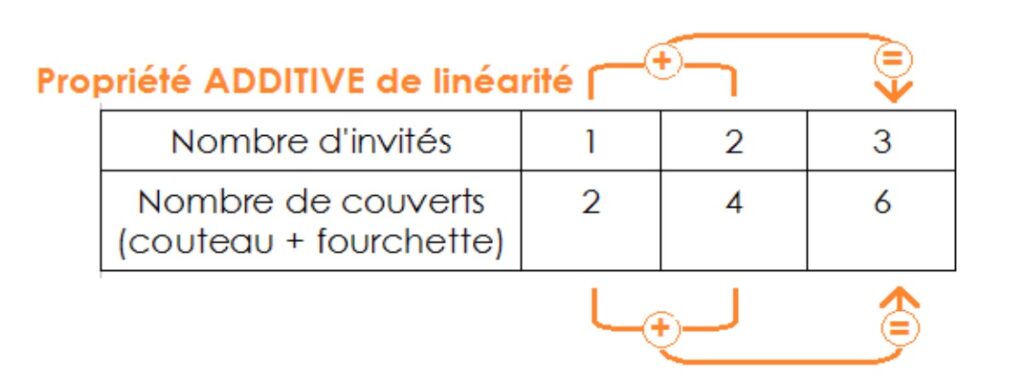
On peut utiliser les propriétés de linéarité dans un tableau de proportionnalité. On remarque sur les données de la première ligne que si l’on additionne 3 et 4, cela donne 7. La propriété de linéarité permet d’additionner ou de soustraire deux colonnes. Si je le fais sur la ligne du haut, je peux le faire sur la seconde ligne : 3,90 + 5,20 = 9,10€
| Quantité | 3 | 4 | 7 |
| Prix | 3.90 | 5.20 | 9,10 |

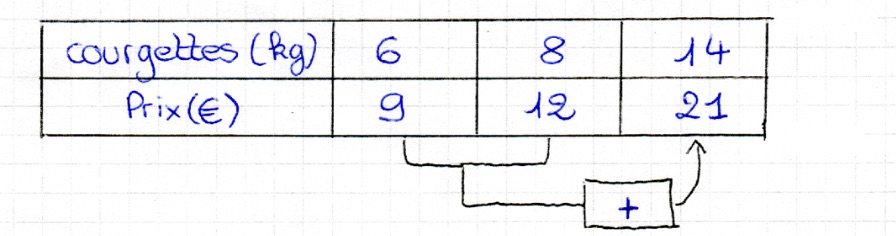
Un producteur de légumes vend des tomates au kilogramme. Lina en achète 6 kg et paye 9 €. Anaëlle en achète 8 kg et paye 12 €. Si Julie achète 14 kg de tomate. Combien devra-t-elle payer ?
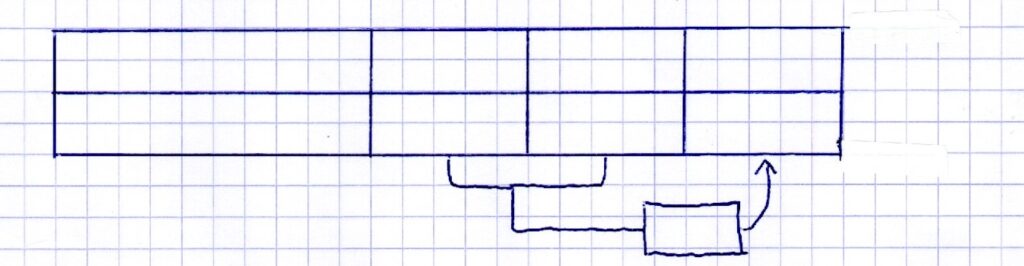
Correction collective avec le groupe classe :
Les élèves vont ensuite résoudre plusieurs situations de proportionnalité en utilisant les propriétés de linéarité de façon individuelle.
Série d’exercices sur les propriétés du tableau de proportionnalité
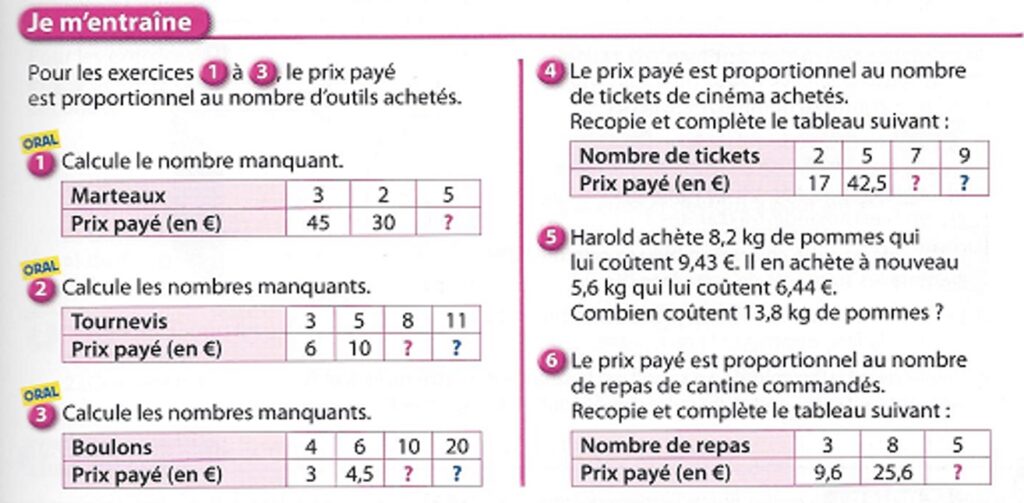
Exercice n°1
| Marteaux | 3 | 2 | 5 |
| Prix (€) | 45 | 30 | 75 |
n°2
| Tournevis | 3 | 5 | 8 | 11 |
| Prix (€) | 6 | 10 | 16 | 22 |
Exercice n°3
| Boulons | 4 | 6 | 10 | 20 |
| Prix (€) | 3 | 4,5 | 7,5 | 15 |
n°4
| Tickets | 2 | 5 | 7 | 9 |
| Prix (€) | 17 | 42,50 | 59,50 | 76,50 |
Exercice n°5
| Pommes (kg) | 8,2 | 5,6 | 13,8 |
| Prix (€) | 9,43 | 6,44 | 15,87 |
n°6
| Repas | 3 | 8 | 5 |
| Prix (€) | 9,6 | 25,6 | 16 |


