Voici la seconde leçon de numération N2 sur les grands nombres entiers supérieurs à 1 000 000. Tu peux retrouver la leçon N1 ici ! Tu peux revenir sur la page d’accueil en cliquant ici !

Les grands nombres permettent de représenter des quantités très importantes, souvent utilisées dans la vie réelle : le nombre d’habitants d’un pays, les distances entre les planètes, ou encore les sommes d’argent dans l’économie. Dans cette leçon, nous allons découvrir et approfondir la connaissance des nombres entiers supérieurs à un million, c’est-à-dire à partir de 1 000 000 et au-delà. Nous apprendrons à les lire, les écrire et les décomposer en utilisant les classes et les rangs (unités, milliers, millions, milliards). Comprendre les grands nombres aide à mieux saisir l’échelle du monde qui nous entoure et à manipuler avec précision les valeurs très élevées en mathématiques comme dans la vie quotidienne.

N2 Les grands nombres

Lire et écrire les grands nombres

Lorsque tu écris un nombre en chiffres, il faut laisser un espace entre les classes pour faciliter la lecture du nombre. Ici nous allons analyser le nombre 5 246 719.

                                     

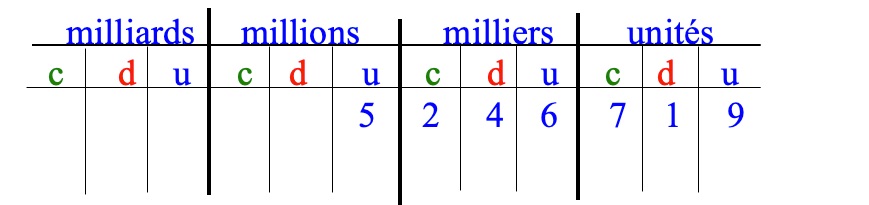
5 246 719  se lit cinq-millions-deux-cent-quarante-six-mille-sept-cent-dix-neuf

Attention ! Mille est invariable

Cent ne prend un « s » seulement lorsqu’il est situé à la fin du nombre.       –> Mille-trois-cents

Les grands nombres : chiffres de et nombres de

5 246 719

2 est le chiffre des centaines de mille 6 est le chiffre des unités simples

5 est le chiffre des unités de millions

52 est le nombre des centaines de milliers. 5 246 est le nombre de milliers.

Décomposer les grands nombres :

Décomposition additive :

Exemple : 8 416 725 = 8 000 000 + 400 000 + 10 000 + 6 000 + 700 + 20 + 5

La décomposition multiplicative avec parenthèses :

Exemple : 8 416 725 = (8 x 1 000 000) + (4 x 100 000) + (1 x 10 000) + (6 x 1 000) + (7 x 100) + (2 x 10) + (5 x 1)

Comparer et ranger les grands nombres entiers

Si deux nombres entiers n’ont pas le même nombre de chiffres, le nombre le plus grand est celui qui a le plus de chiffres.

Si deux nombres entiers ont le même nombre de chiffres, on compare les chiffres un à un de gauche à droite.

Exemples : 9 025 453 > 8 025 914          car 9 > 8 8 453 058 < 8 914 058          car 4 < 9

Ranger dans l’ordre croissant, c’est ranger du plus petit au plus grand ! 0 < 1 < 2

Exemple :       1 000 < 525 000 < 650 200 < 750 980 < 1 000 000 < 22 500 800

Ranger dans l’ordre décroissant, c’est ranger du plus grand au plus petit ! 2 > 1 > 0

Exemple :       22 500 800 > 1 000 000  >  750 980  > 650 200   >  525 000   > 1 000

Encadrer et intercaler les grands nombres

On peut encadrer à la dizaine près : 7 252 363 (exemple complexe)

Dans un premier temps, on recherche le chiffre des dizaines : 7 252 363. Ensuite, on trouve le nombre de dizaines : 7 252 363. Il s’agit du nombre de paquets de 10 que l’on peut faire. On peut faire 725 236 paquets puis on positionne le zéro des unités. –> 7 252 360 On a ainsi 7 252 360 < 252 363 < ?

Comme nous encadrons à la dizaine près, on avance donc de 10 en 10. On ajoute alors une dizaine supplémentaire, il y a donc 725 237 paquets. On positionne alors le zéro des unités. –> 7 252 370

7 252 360 < 252 363 < 7 252 370

Intercaler des nombres consiste à placer un ou plusieurs nombres entre deux nombres donnés pour respecter l’ordre croissant. Avec les grands nombres, cela permet de mieux comprendre leur taille et leur position sur la droite numérique. Par exemple, entre 7 000 000 et 7 000 010, on peut intercaler 7 000 001, 7 000 002, 7 000 003… et ainsi de suite. Cette activité aide à comparer, ranger et repérer les nombres très grands. Intercaler des nombres développe aussi la maîtrise des unités, dizaines, centaines, milliers et millions, car il faut observer précisément chaque chiffre pour trouver les nombres intermédiaires corrects. C’est un outil essentiel pour manipuler les grands nombres avec précision.

Les compétences à travailler sur les grands nombres entiers

Compétence sur les grands nombres	Indicateur de réussite (ce que l’élève sait faire)	Lien programme / ressource officielle
Lire et écrire les nombres entiers jusqu’au million et au-delà	L’élève lit correctement les nombres (ex : 456 321 → « quatre cent cinquante-six mille trois cent vingt-et-un ») et sait les écrire en chiffres et en lettres	Programme cycle 3 – Mathématiques (BO 17 avril 2025)
Comparer et ranger des nombres entiers	L’élève sait dire quel nombre est le plus grand ou le plus petit, et ranger une liste de nombres du plus petit au plus grand	Programme cycle 3 – Mathématiques (BO 17 avril 2025)
Décomposer un nombre selon les valeurs de position	L’élève décompose un nombre selon ses unités, dizaines, centaines, milliers, millions (ex : 456 321 = 4×100 000 + 5×10 000 + 6×1 000 + 3×100 + 2×10 + 1×1)	Ressources cycle 3 – Mathématiques, décomposition des nombres
Utiliser les grands nombres dans des situations concrètes	L’élève applique les nombres pour décrire des populations, distances, sommes d’argent, etc., et les manipule correctement	Programme cycle 3 – Mathématiques (BO 17 avril 2025)
Repérer et utiliser les ordres de grandeur	L’élève estime si un nombre est petit ou très grand, compare des millions, milliards, et comprend l’échelle des nombres	Programme cycle 3 – Mathématiques (BO 17 avril 2025)

https://www.youtube.com/@soscartables