Voici la leçon CP5 sur les situations de partage. Tu peux retrouver la dernière leçon ici ! Tu peux revenir sur la page d’accueil ici !
CP5 Les situations de partage
Problème n°1 : Les situations de partage (partition)
Dans certaines situations, on est amené à faire des partages.
28 oiseaux sont placés dans 4 cages différentes. Combien y a-t-il d’oiseaux par cage ? En restera-t-il dans la volière ?
Je cherche le nombre d’oiseaux par cage :
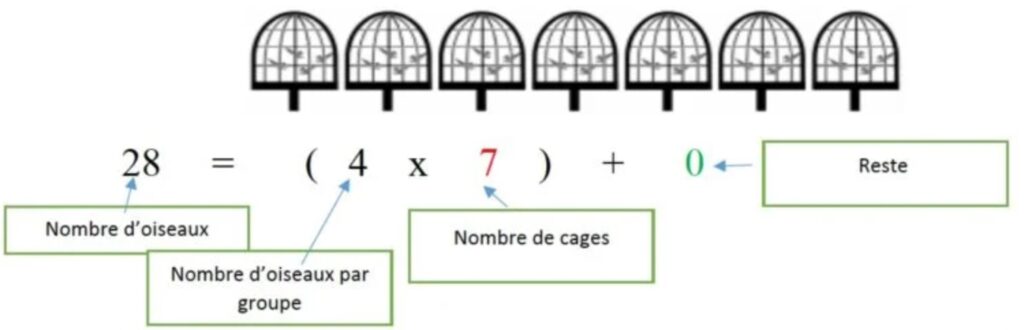
28 = ( 4 x 7 ) + 0

On peut mettre 7 oiseaux par cage. Il n’en restera aucun dans la volière.
Problème n°2 : Situation de partition
31 oiseaux sont placés dans 4 cages différentes. Combien y a-t-il d’oiseaux par cage ? En restera-t-il dans la volière ?
Je cherche le nombre d’oiseaux par cage :
31 = ( 4 x 7 ) + 3

On peut mettre 7 oiseaux par cage. Il en restera 3 dans la volière.
Problème n°3 : Les situations de partage (quotition)
Dans certaines situations, on est amené à faire des regroupements.
28 oiseaux sont répartis en groupes de 4. Combien faut-il de cages ? En restera-t-il dans la volière ?
Je cherche le nombre de cages utilisés:
28 = ( 4 x 7 ) + 0
Il faut 7 cages pour les oiseaux. Il n’en restera aucun dans la volière.
| Type de division | On connaît… | On cherche… | Exemple |
|---|---|---|---|
| Partition | Total et nombre de parts | Taille d’une part | 12 ÷ 4 = 3 |
| Quotition | Total et taille d’un groupe | Nombre de groupes | 12 ÷ 3 = 4 |
Situation de partition (ou partage)
Il s’agit de répartir équitablement une quantité totale entre un certain nombre de parts (ou de personnes, de groupes, etc.). C’est la division par le nombre de parts.
Une situation de partition, ou de partage, consiste à répartir une quantité totale de manière équitable entre plusieurs parts, personnes ou groupes. Il s’agit essentiellement de diviser ce que l’on possède pour que chacun reçoive une part égale. Cette situation se rencontre dans la vie quotidienne : partager des bonbons entre amis, répartir un budget ou distribuer des tâches. Pour résoudre ce type de problème, on divise la quantité totale par le nombre de parts souhaité. Ainsi, chaque individu obtient la même portion. L’important est de s’assurer que le partage est juste et équilibré, et que chacun reçoit exactement ce qui lui revient, sans différence ni favoritisme.
Situation de quotition (ou groupement)
Il s’agit de former un certain nombre de groupes à partir d’une quantité totale, en connaissant la taille de chaque groupe. C’est la division par la taille d’un groupe.
Une situation de quotition consiste à former un certain nombre de groupes à partir d’une quantité totale, en connaissant la taille de chaque groupe. Contrairement au partage où l’on cherche la part individuelle, ici on cherche combien de groupes on peut constituer. Cette situation se rencontre fréquemment : organiser des équipes pour un jeu, ranger des livres par étagères ou distribuer des objets par lots. Pour résoudre ce type de problème, on divise la quantité totale par la taille d’un groupe. Ainsi, on obtient le nombre exact de groupes possibles. L’essentiel est de s’assurer que chaque groupe ait la même taille, sans restes ni inégalités.
Quelles compétences sont travaillées pour les élèves de CM1 CM2 sur les situations de partage ?
| Domaine : les situations de partage | Compétence liée au partage / à la division | Exemple d’application en situation de partage |
|---|---|---|
| Nombres, calcul et résolution de problèmes | Modéliser les situations de partage équitables | L’élève comprend qu’un problème de « partager 12 bonbons entre 4 enfants » peut se modéliser par la division 12 ÷ 4. |
| Nombres, calcul et résolution de problèmes | Raisonner sur le sens de la division | L’élève vérifie que le partage est bien équitable : « si chaque enfant a 3 bonbons, est-ce que ça fait bien 12 au total ? » |
| Nombres, calcul et résolution de problèmes | Calculer avec des nombres entiers et des fractions simples | L’élève effectue la division posée ou mentale : 12 ÷ 4 = 3, ou partage 5/6 de tarte entre 3 amis (≈ 5/18 chacun). |
| Organisation et gestion de données | Représenter le partage sous forme de schéma, diagramme ou dessin | L’élève dessine 12 bonbons répartis dans 4 groupes, ou utilise des barres/fractions pour montrer la répartition. |
| Résolution de problèmes (transversal) | Communiquer la démarche et la solution | L’élève explique à l’oral ou à l’écrit comment il a fait le partage : « j’ai dessiné, j’ai compté, chaque groupe a 3 bonbons » ; il peut aussi argumenter face à une autre solution. |



Ping : La division : leçon CM1