Dans cette leçon de numération pour les élèves de CM1–CM2, nous allons travailler sur les nombres décimaux. Les élèves découvriront qu’un nombre décimal est un nombre qui peut s’écrire avec une virgule et qui correspond à un partage en dixièmes, centièmes, millièmes, etc., comme 3,4 ou 12,75. Ils apprendront à distinguer la partie entière et la partie décimale, à lire et écrire ces nombres, à les placer sur une droite graduée et à les relier à des situations de mesure (longueurs, masses, prix…).. Tu pourras relire la leçon précédente ici ! Tu peux revenir sur la page d’accueil en cliquant ici !
N6-N7 Les nombres décimaux
Ecrire les nombres décimaux
Un nombre décimal peut s’écrire sous forme de fraction décimale ou avec une virgule.
| Fraction | Signification | Écriture à virgule | Lecture |
|---|---|---|---|
| 1/10 | 1 : 10 l’unité est divisée en 10 | 0,1 | un dixième |
| 1/100 | 1 : 100 l’unité est divisée en 100 | 0,01 | un centième |
| 1/1 000 | 1 : 1 000 l’unité est divisée en 1 000 | 0,001 | un millième |
| 1/10 000 | 1 : 10 000 l’unité est divisée en 10 000 | 0,0001 | un dix-millième |
Lire les nombres décimaux

La virgule est toujours placée après le chiffre des unités.
| Partie entière | Virgule | Partie décimale |
|---|---|---|
| 15 | , | 628 |
À gauche de la virgule, c’est la partie entière.
À droite de la virgule, c’est la partie décimale.
On peut lire :
- « quinze virgule six-cent-vingt-huit »
- « quinze et six-cent-vingt-huit millièmes »
- « quinze-mille-six-cent-vingt-huit millièmes »
Placer les nombres décimaux dans un tableau
Pour pouvoir écrire les nombres décimaux, il faut rajouter des colonnes à droite du tableau des entiers.
| 10 000 | 1 000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1 000 | 1/10 000 |
|---|---|---|---|---|---|---|---|---|
| dizaines de mille | unités de mille | centaines | dizaines | unités | dixièmes | centièmes | millièmes | dix-millièmes |
| 0 | 0 | 3 | 0 | 5 | 6 | 2 | 0 | 0 |
Ce nombre s’écrit 305,62. On n’écrit pas les zéros à gauche de la partie entière, ni les zéros à droite de la partie décimale.
Décomposer un nombre décimal
- Décomposition : partie entière / partie décimale –> 37,642= 37 + 0,642
- Décomposition additive –> 37,642 = 30 + 7+ 0,6 + 0,04 + 0,002
- Décomposition multiplicative –> 37,642 = (3X10)+ (7×1) + (6X0,1)+(4X0,01)+(2X0,001)
Comparer et ranger des nombres décimaux
Pour comparer deux nombres décimaux, il faut penser à la valeur de chaque chiffre.
Il faut d’abord comparer la partie entière : 12,5<15,6 car 12<15
Si la partie entière est égale alors il faut regarder la partie décimale : 6,3 < 6,4 car 3<4
S’il n’y a pas le même nombre de chiffre au niveau de la partie décimale pour les 2 nombres, on positionne des « 0 » à droite (dans la partie décimale) pour que cela soit le cas.
Ex : 0,34 < 0,4 car 0,34 < 0,40 (en effet 4 dixièmes correspondent à 40 centièmes)
Autre exemple : 1,6>1,321 car 1,600>1,321 car 600 millièmes > 321 millièmes
Encadrer des nombres décimaux
Pour encadrer un nombre décimal entre deux nombres décimaux, on cherche le nombre qui le précède (avant) et le nombre qui le suit (après). On peut encadrer entre deux entiers 5 < 5,64 < 6 ou entre deux dixièmes 5,6 < 5,64 < 5,7
Placer des nombres décimaux sur une droite graduée
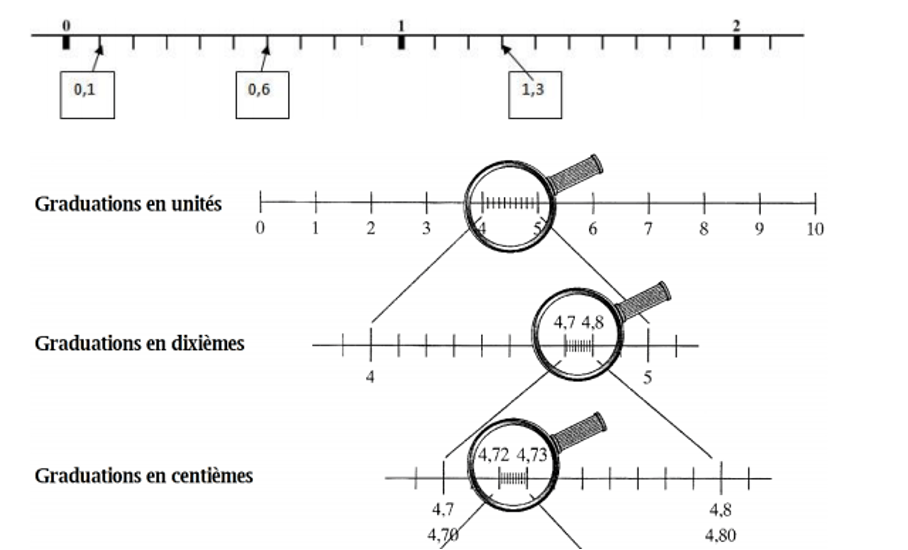
Les nombres décimaux sont un type de nombre utilisé dans les mathématiques pour représenter des valeurs non entières, c’est-à-dire des fractions ou des parties d’un tout.
Dans un premier temps, nous allons définir la notion de « nombre décimal ». On indiquera comment on peut transformer une fraction décimale en un nombre décimal et inversement.
Le groupe classe apprendra à les lire et à les écrire avec des mots importants comme « dizaine », « unité », « dixième », « centième » ou « millième ». On verra qu’il y a plusieurs façons d’écrire un nombre décimal : 5,023
cinq virgule zéro-vingt-trois
cinq unités et vingt-trois millièmes
cinq-mille-vingt-trois millièmes
On travaillera à nouveau la valeur positionnelle des chiffres et le nombre de centaines par exemple.
Le groupe classe apprendra ensuite à décomposer de façon additive et multiplicative des nombres décimaux.
10,602 = 10 + 0,6 + 0,002 = (1×10) + (6×0,1) + (2×0,001)
Par la suite, on pourra comparer et ranger les nombres dans l’ordre croissant ou décroissant. On pourra également les nombres à l’unité près, à la dizaine de mille près, à la centaine de millions près…
L’utilisation des droites graduées est très importante en CM2 pour développer la compréhension des nombres décimaux et leur positionnement précis sur une échelle numérique. Les élèves apprennent à analyser une droite graduée en identifiant l’origine, l’unité, l’échelle et les graduations intermédiaires, puis à replacer des nombres comme 2,3 ; 1,75 ou 4,2 avec exactitude.
Quelles compétences sont travaillées pour les élèves de CM1 CM2 sur les nombres décimaux ?
| Compétence | Indicateur de réussite | Lien vers une ressource |
|---|---|---|
| Comprendre les nombres décimaux | L’élève sait qu’un nombre décimal exprime des quantités entre entiers (2,5 kg, 1,25 €). | Leçon Numération M10 : Nombres décimaux – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |
| Lire et écrire les décimaux | L’élève lit/écrit : 3,14 → trois virgule quatorze ; 0,75 → zéro virgule soixante-quinze. | Nombres décimaux – SOS Cartables ; Mathématiques CM2 – SOS Cartables. |
| Placer sur une droite graduée | L’élève situe : 1,2 entre 1 et 2 ; 2,75 entre 2 et 3. | Leçon Numération M10 : Nombres décimaux – SOS Cartables ; Droite graduée CM2 – SOS Cartables. |
| Comparer et ranger décimaux | L’élève compare : 2,3 < 2,35 < 2,4 ; ranger 1,8 ; 0,95 ; 1,02. | Comparaison décimaux – SOS Cartables ; Programme cycle 3 – Éduscol. |
| Additionner/soustraire décimaux | L’élève calcule : 1,2 + 3,45 = 4,65 ; 5,6 – 2,34 = 3,26. | Exercices décimaux Série 1 – SOS Cartables ; Nombres décimaux CM2 – SOS Cartables. |
| Appliquer en problèmes | L’élève résout : 2,5 kg de pommes + 1,75 kg = ? kg au total. | Nombres décimaux – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |
📚 Lexique interactif : Les nombres décimaux
| Compétence | Indicateur de réussite |
|---|---|
| Comparer décimaux | L’élève range 2,3 ; 1,89 ; 2,31 en croissant : 1,89 < 2,3 < 2,31. |
| Ranger sur droite | L’élève place et ordonne 4,5 ; 3,2 ; 4,8 sur droite graduée. |
| Arrondir unité près | L’élève arrondit 7,64 → 8 et justifie (dixième 6 ≥ 5). |
| Arrondir dizaine mille | L’élève arrondit 123 456 → 120 000 (dix-millier 4 < 5). |
| Arrondir cent millions | L’élève arrondit 456 789 123 → 500 000 000 (cent millions 4 < 5). |
| Appliquer en contexte | L’élève compare distances et arrondit : 2,347 km ≈ 2 km. |


Ping : Exercices d'application sur la décomposition des décimaux
Ping : les nombres décimaux : chiffre - nombre - décomposition
Ping : Les nombres décimaux
Ping : Les nombres décimaux - droites graduées - CM2
Ping : Nombres décimaux
Ping : Droites graduées et nombres décimaux (2) CM1/CM2
Ping : N6 Vers les nombres décimaux (1)