Résoudre des problèmes de longueurs est essentiel au cycle 3. Les exercices sur les longueurs en CM1‑CM2 permettent aux élèves d’apprendre à utiliser les unités de mesure du système métrique (millimètre, centimètre, mètre, kilomètre) et à passer de l’une à l’autre grâce aux conversions.
Dans cet article, je vous propose des exercices pour donner du sens à ces notions. Retrouvez la leçon ici ! Tu peux revenir sur la page d’accueil en cliquant ici !
Série 1 : Problèmes de longueurs
Une histoire de ponts
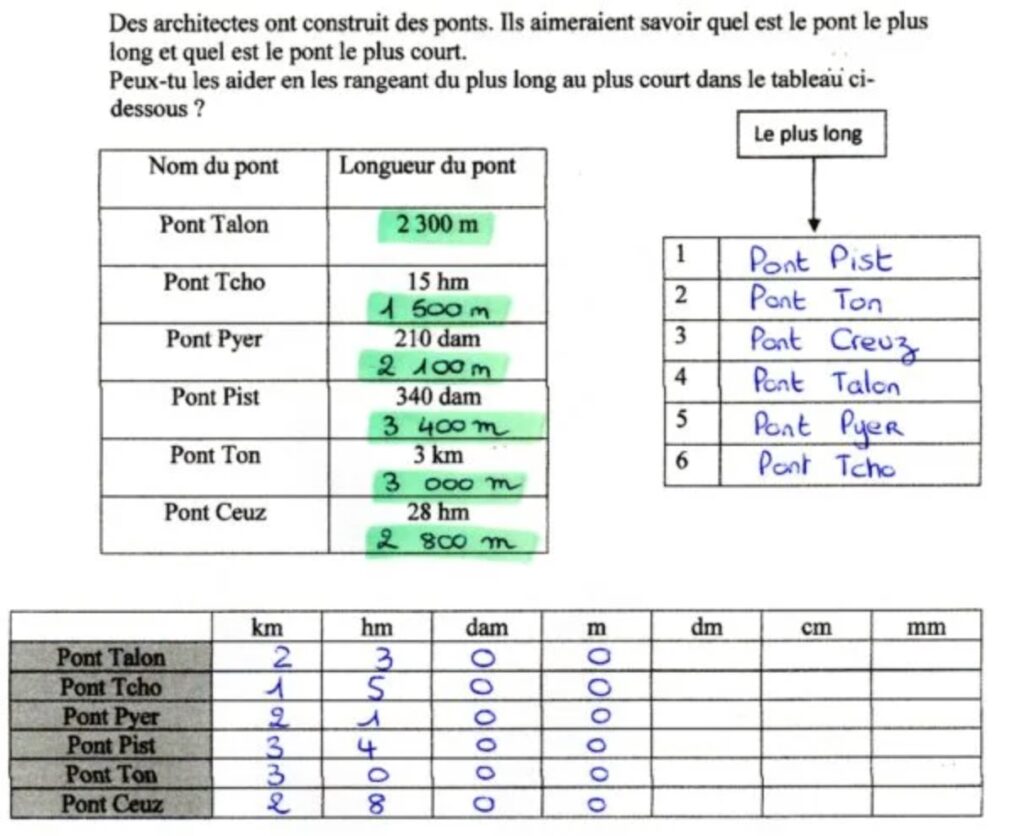
Des architectes ont construit des ponts. Ils aimeraient savoir quel est le pont le plus long et quel est le pont le plus court. Peux-tu les aider en les rangeant du plus long au plus court dans le tableau ci-dessous ?
| Nom du pont | Longueur du pont |
| Pont Talon | 2 300 m |
| Pont Tcho | 15 hm |
| Pont Pyer | 210 dam |
| Pont Pist | 340 dam |
| Pont Ton | 3 km |
| Pont Ceuz | 28 hm |
| km | hm | dam | m | dm | cm | mm | |
| Pont Talon | |||||||
| Pont Tcho | |||||||
| Pont Pyer | |||||||
| Pont Pist | |||||||
| Pont Ton | |||||||
| Pont Ceuz |
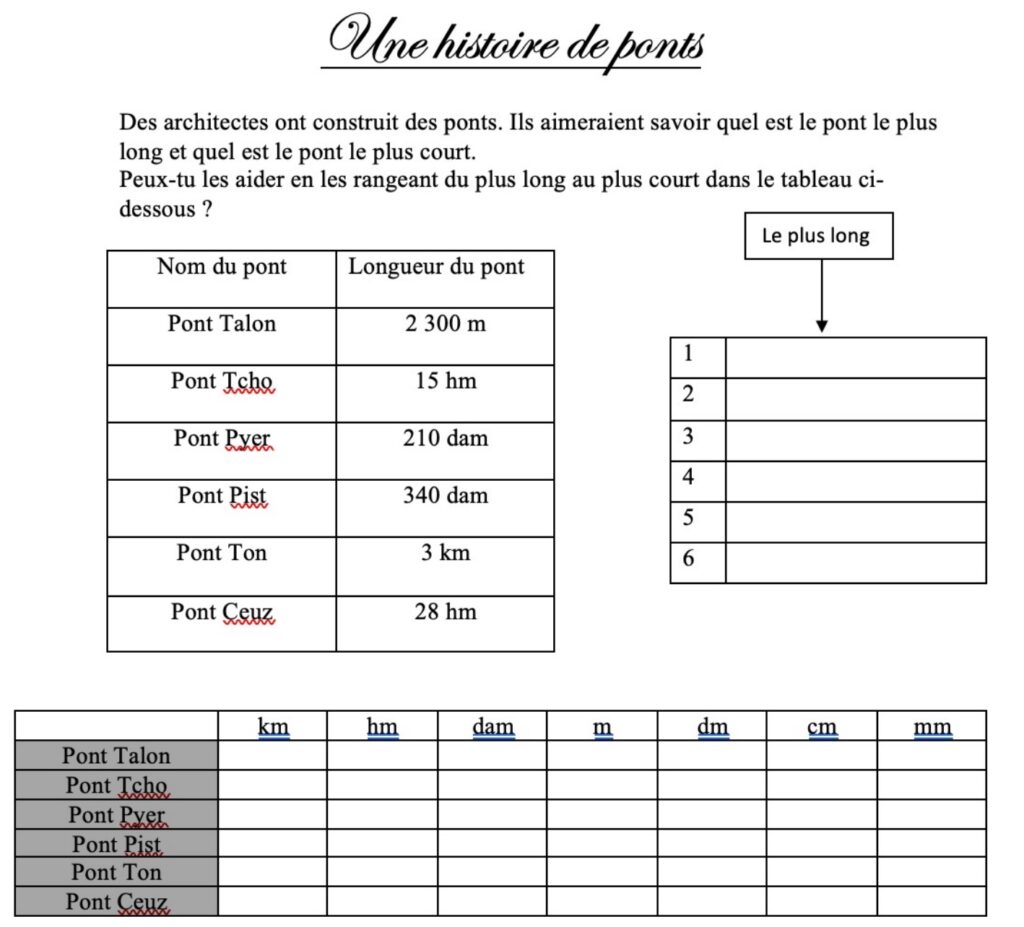
Série 1 : Correction des problèmes de longueurs
Série 2 : Problèmes de longueurs
Problème 1
Jeudi, lors du cross, les CM2 ont parcouru 1 600 m. Pendant ce temps, les CE1 ont fait un parcours de 1 km. Quelle distance supplémentaire les CM2 ont-ils parcourue ? (par rapport aux CE1)
Problème 2
Théo a fait une promenade en vélo en trois étapes de longueurs différentes.
Étape 1 : 325 dam Étape 2 : 34 hm Étape 3 : 2 850 m
Quelle est la distance totale parcourue par Théo ?
Problème 3
Dans un morceau de grillage de 15 m, on a coupé un morceau de 120 cm et un morceau de 380 cm. 1/ Quelle longueur a-t-on déjà utilisée ? Quelle longueur de grillage reste-t-il ?
Problème 4
Les organisateurs d’un triathlon ont prévu ainsi les trois épreuves :
– un parcours de natation de 1 500 m
– un parcours de vélo de 85 hm
– un cross.
Au total, chaque concurrent aura parcouru 18 km. Quelle est la distance parcourue lors du cross ?
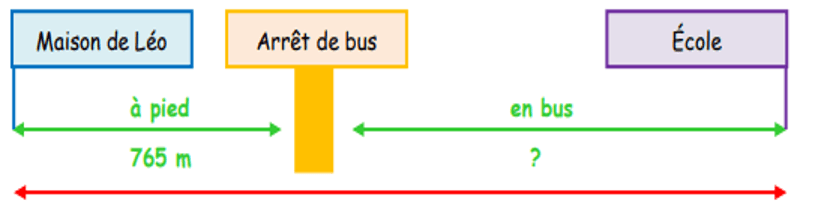
Quelle distance Léo parcourt-il à pied, aller-retour, chaque jour ?
Série 2 : Correction des problèmes de longueurs
Problème 1
Je cherche la distance supplémentaire parcourue par les cm2 :
Conversion : 1 km = 1 000 m
Calculs : 1 600 m – 1 000 m = 600 m
Les CM2 ont parcouru 600 m de plus.
Problème 2
Je cherche la distance totale parcourue par Théo :
Conversion : 325 dam = 3 250 m 34 hm = 3 400 m
Calculs : 3 250 m + 3 400 m + 2 850 m = 9 500 m
Théo a parcouru 9 500 m.
Problème 3
1/ Je cherche la longueur utilisée :
Calculs : 120 cm + 380 cm = 500 m
On a utilisé 500 cm de grillage.
2/ Je cherche la longueur restante :
Conversion : 15 m = 1 500 cm ou 500 cm = 5 m
Calculs : 15 m – 5 m = 10 m ou 1 500 cm – 500 cm = 1 000 cm
Il reste 10 m (1 000 cm) de grillage.
Problème 4
1/ Je cherche la distance effectuée sans le cross :
Conversion : 85 hm = 8 500 m
Calculs : 8 500 cm + 1 500 m = 10 000 m = 10 km
Les parcours de natation et de cyclisme ont une distance de 10km.
2/ Je cherche la distance du cross :
Calculs : 18 km – 10 km = 8 km
La distance parcourue lors du cross est de 8 km.
Problème 5
1/ Je cherche la distance entre l’arrêt de bus et l’école :
Conversion : 6 km = 6 000 m
Calculs : 6 000 m – 765 m = 5 235 m
Il y a 5 235 m entre l’arrêt de bus et l’école.
2/ Je cherche la distance parcourue à pied aller-retour :
Calculs : 765 m x 2 = 1 530 m ou 765 m + 765 m = 1 530 m
La distance parcourue à pied est de 1 530 m.
Série 3 : Problèmes de longueurs

Série 3 : Correction des problèmes de longueurs
Problème 1
Je cherche le nombre de bonds :
• 4,95 m = 495 cm
• 55 cm 495 = (55 × 9)
La grenouille devra faire 9 bonds.
Problème 2
Je cherche la longueur restante :
• 5 m = 500 cm
• 27 cm
• 1,75 m = 175 cm
• 0,38 m = 38 cm
• 9,4 dm = 94 cm
27 cm + 175 cm + 38 cm + 94 cm = 334 cm
500 cm − 334 cm = 166 cm
Il reste 1,66 m (166 cm) de ruban.
Problème 3 : problèmes de longueurs
Je cherche la distance « arrêt de bus – école » :
• 8,55 km = 8 550 m
• 765 m
8 550 m − 765 m = 7 785 m
La distance est de 7,785 km (7 785 m).
Je cherche la distance parcourue à pied :
765 m × 2 = 1 530 m = 1,53 km
Elle parcourt 1,53 km à pied.
Problème 4 : problèmes de longueurs
Etna : 3,34 dam 5 m = 3 345 m
Meru : 4 km 5 hm 6 dam 6 m = 4 566 m
Aconcagua : 69 hm 59 m = 6 959 m
Kerinci : 38 hm = 3 800 m
Erebus : 379 dam 4 m = 3 794 m
Etna < Erebus < Kerinci < Meru < Aconcagua
Problème 5 : problèmes de longueurs
Le nez de Pinocchio
1 048 576 cm = 10 485,76 m = 10,48576 km

Quelles compétences travaille-t-on pour convertir des longueurs ?
| Compétence : Problèmes de longueurs | Indicateur de réussite : Problèmes de longueurs |
|---|---|
| Lire et choisir l’unité adaptée (cm, m, mm) | L’élève mesure un objet (crayon : 15 cm ; table : 1,20 m) et sait qu’on n’exprime pas 5 km en mètres ni 3 m en mm. |
| Convertir entre unités (mm ↔ cm ↔ m ↔ km) convertir des longueurs | L’élève calcule : 1 m = 100 cm = 1000 mm ; 2,5 m = 250 cm ; 3000 m = 3 km et réciproquement. |
| Comparer et ranger des longueurs | L’élève range 45 cm, 1 m 20, 95 cm, 2 m par ordre croissant et complète : 1 m 50 > __ cm. |
| Résoudre des problèmes de longueur additifs/soustractifs | L’élève résout : « Le fil A fait 3 m 45, B fait 2 m 80. Quelle longueur pour les deux ? » (6 m 25). |


