Dans cette leçon de géométrie pour les élèves de CM1–CM2, nous allons travailler sur les cercles. Les élèves découvriront qu’un cercle est l’ensemble des points situés à égale distance d’un point appelé centre, et que cette distance s’appelle le rayon. Ils apprendront à tracer des cercles au compas, à utiliser et nommer les éléments du cercle (centre, rayon, diamètre, corde, arc) et à faire la différence entre le cercle (ligne) et le disque (surface).
Tu peux revenir sur la page d’accueil en cliquant ici !
Géom 12 : Les cercles
Définition
Un cercle est une figure dont tous les points sont situés à la même distance d’un point appelé centre.
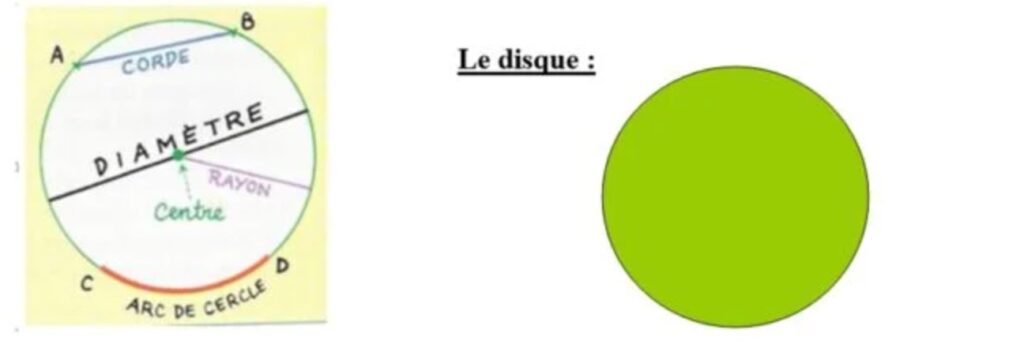
Vocabulaire géométrique sur le cercle
Le rayon est la distance entre un point du cercle et le centre.
Le diamètre est un segment reliant deux points opposés du cercle et passant par le centre. C’est le double du rayon. diamètre = rayon x 2
Une corde est un segment reliant deux points du cercle sans passer par le centre.
Un arc de cercle est une portion du cercle.
Le disque est la surface située à l’intérieur du cercle.
Lexique : Les cercles
Cercle
Ensemble des points qui sont à la même distance d’un point appelé centre.
Centre
Le point fixe situé au milieu du cercle, d’où l’on mesure la distance jusqu’à la bordure.
Rayon
Segment qui va du centre à la bordure du cercle; sa longueur est le rayon.
Diamètre
Segment qui passe par le centre et relie deux points opposés de la bordure; il mesure deux rayons.
Corde
Segment qui relie deux points quelconques de la bordure du cercle (sans forcément passer par le centre).
Arc de cercle
Partie de la bordure du cercle située entre deux points de la circonférence.
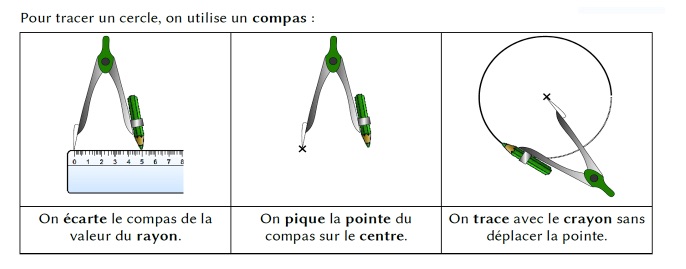
Comment construire les cercles ?
Pour tracer un cercle, on se sert d’un compas. D’abord, on choisit un point sur la feuille : c’est le centre du cercle. On le marque avec une petite croix et on l’appelle souvent O. Ensuite, on écarte le compas de la longueur du rayon, c’est-à-dire la distance entre le centre et la bordure du cercle. On plante la pointe métallique du compas sur le centre et, sans la bouger, on fait tourner doucement le crayon autour. Le trait doit revenir exactement au point de départ. Si l’on reste bien stable, on obtient un cercle parfait et régulier.
Quelles compétences travaille-t-on autour des cercles ?
| Compétence | Indicateur de réussite | Lien vers une ressource |
|---|---|---|
| Comprendre le cercle | L’élève sait qu’un cercle est une figure plane limitée par une courbe fermée (centre, rayon, diamètre). | Leçon Géométrie G13 : Les cercles – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |
| Identifier centre/rayon/diamètre | L’élève repère : rayon = distance centre-bord ; diamètre = 2 rayons. | Cercles CM1/CM2 – SOS Cartables ; Géométrie CM2 – SOS Cartables. |
| Reproduire un cercle | L’élève trace un cercle avec compas (rayon donné). | Leçon Géométrie G13 : Les cercles – SOS Cartables ; Programme cycle 3 – Éduscol. |
| Mesurer circonférence/rayon | L’élève mesure : rayon 5 cm → diamètre 10 cm. | Reproduction cercles – SOS Cartables ; Mathématiques CM2 – SOS Cartables. |
| Comparer cercles | L’élève compare : cercle rayon 3 cm < cercle rayon 5 cm. | Exercices cercles Série 1 – SOS Cartables ; Cercles CM2 – SOS Cartables. |
| Appliquer en problèmes | L’élève calcule : diamètre 12 cm → rayon 6 cm. | Cercles – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. |


