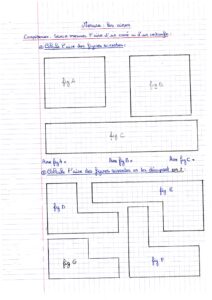
Nous travaillons aujourd’hui la leçon sur les périmètres. Tu peux retrouver la leçon précédente ici ! Clique ici pour revenir sur la page d’accueil !
M2 Les périmètres
Définition des périmètres
Le périmètre d’une figure est la longueur du contour de cette figure. C’est le calcul du contour d’un polygone.
Calculer le périmètre d’un polygone
Pour calculer le périmètre d’un polygone quelconque, on additionne les longueurs de tous ses côtés. Voici un polygone quelconque :
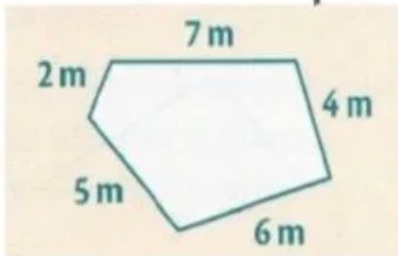
Périmètre = 7 m + 4 m + 6 m + 5 m + 2 m = 24 m
Le périmètre de ce polygone est de 24 m.
Quelles compétences sont travaillées pour les élèves de CM1 CM2 sur les périmètres ?
| Compétence sur les périmètres | Indicateur de réussite (ce que l’élève sait faire) | Lien programme / ressource officielle |
|---|---|---|
| Identifier le périmètre d’une figure géométrique | L’élève sait que le périmètre correspond à la longueur du contour d’une figure | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Calculer le périmètre d’un polygone régulier (carré, rectangle, triangle…) | L’élève applique correctement les formules de périmètre selon les figures étudiées | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Estimer ou comparer des périmètres | L’élève compare deux figures selon leur contour et justifie ses choix | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Résoudre des problèmes impliquant le périmètre | L’élève choisit et utilise la bonne formule ou stratégie pour résoudre des situations de la vie courante (clôture, cadre, parcours, etc.) | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Relier le périmètre à d’autres grandeurs (aires, longueurs…) | L’élève distingue clairement le périmètre d’autres notions et peut expliquer la différence entre aire et périmètre | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
Histoire des périmètres
Le périmètre d’une figure, c’est la longueur de son contour. Pour le trouver, on additionne les longueurs de tous les côtés. Par exemple, si on veut connaître le périmètre d’un carré dont chaque côté mesure 4 cm, on fait 4 + 4 + 4 + 4 = 16 cm. Le périmètre sert à savoir combien il faut de bordure, de clôture ou de ruban pour faire le tour d’une forme. Il s’exprime toujours dans une unité de longueur : centimètre, mètre, kilomètre… selon la taille de la figure qu’on étudie.
Le périmètre est une notion très ancienne. Déjà, les anciens Égyptiens l’utilisaient pour mesurer leurs champs et construire les pyramides avec précision. Le mot « périmètre » vient du grec : « peri » signifie « autour » et « metron » veut dire « mesure ». Donc, périmètre veut dire mesurer autour d’une figure. Aujourd’hui, le périmètre nous aide à savoir combien il faut de clôture, de ruban ou de bordure pour entourer quelque chose. Il s’applique à toutes sortes de formes : carrés, rectangles, triangles ou polygones. Comprendre cette notion permet de mieux calculer et organiser l’espace autour de nous.
Dans la vie de tous les jours, nous utilisons le périmètre sans toujours nous en rendre compte. Par exemple, pour mesurer le tour d’un terrain de sport, le bord d’un jardin ou la bande d’un cadre, on calcule le périmètre. On additionne les longueurs de tous les côtés pour obtenir la distance totale autour de la figure. Savoir mesurer le périmètre aide à résoudre des problèmes concrets et à mieux observer notre environnement. Cette compétence est utile pour les jeux, les constructions et même certains travaux à la maison ou à l’école.
Pour aller plus loin sur les périmètres !
| Figure | Formule du périmètre | Exemple |
|---|---|---|
| Carré | 4 × côté | si côté = 5 cm → P = 4 × 5 cm = 20 cm |
| Rectangle | 2 × (longueur + largeur) | si L = 8 cm, l = 3 cm → P = 2 × (8 cm + 3 cm) = 22 cm |
| Triangle | somme des 3 côtés | si côtés = 4 cm, 5 cm et 6 cm → P = 4 cm + 5 cm + 6 cm = 15 cm |
| Polygone | somme de tous les côtés | ajouter chaque longueur mesurée |
Ne pas confonde Périmètres et Aires !
Lis correctement la consigne pour éviter de les confondre.
Quelles compétences sont travaillées pour les élèves de CM1 CM2 sur les périmètres ?
| Compétence | Indicateur de réussite | Lien vers une ressource |
|---|---|---|
| Comprendre la notion de périmètre | L’élève sait que le périmètre est la somme des longueurs des côtés d’une figure (tour d’un polygone). | Leçon M2 : Les périmètres – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. eduscol.education |
| Mesurer le périmètre d’un polygone | L’élève mesure et additionne : rectangle 5+3+5+3=16 cm. | |
| Appliquer les formules de base | L’élève calcule : carré P=c×4 ; rectangle P=(L+l)×2 ; triangle P=sum côtés. | Leçon M2 : Les périmètres – SOS Cartables ; Grandeurs et mesures CM2 – SOS Cartables. sos-cartables |
| Comparer des périmètres | L’élève compare : figure A (12 cm) < figure B (15 cm). | |
| Calculer en problèmes concrets | L’élève résout : Un jardin mesure 10m×6m, quel est son périmètre ? | Exercices périmètres Série 1 – SOS Cartables ; Périmètre CM1/CM2 – Pass Education. pass-education |
| Distinguer périmètre et aire | L’élève différencie : périmètre = longueur tour, aire = surface intérieure. | Périmètre – SOS Cartables ; Programme mathématiques cycle 3 – Éduscol. eduscol.education |