Nous travaillons aujourd’hui la leçon sur les aires. Tu peux retrouver la leçon précédente ici ! Clique ici pour revenir sur la page d’accueil !
M3 Les aires
Définition des aires
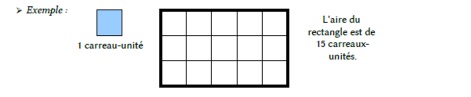
Mesurer l’aire (l’étendue) d’une surface plane, c’est savoir combien il faut de surfaces-unités pour la recouvrir complètement.
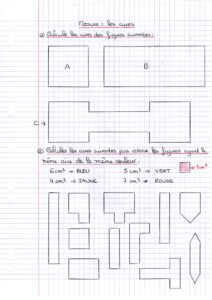
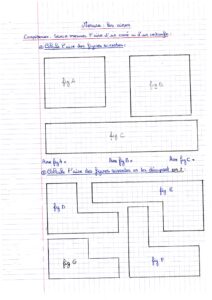
Mesurer et comparer des aires
Pour mesurer l’aire (l’étendue) d’une figure, il faut compter le nombre d’unités qu’il faut pour la recouvrir entièrement.

Certaines surfaces peuvent avoir la même aire. De plus, si deux surfaces se superposent exactement, elles ont la même aire.

Les unités d’aire
L’unité principale de mesure d’aire est le mètre carré. C’est l’aire d’un carré dont chaque côté mesure 1 mètre. On peut l’imaginer comme une grande case de 1 m × 1 m, utilisée comme unité pour mesurer des surfaces. On l’écrit m².
Le mètre carré sert à mesurer des surfaces assez grandes : une pièce, un mur, un jardin, une cour d’école… Plus la surface est grande, plus on utilise souvent des multiples du mètre carré, comme les dizaines, centaines ou milliers de mètres carrés. Pour des surfaces plus petites, on utilise au contraire des unités plus petites : le décimètre carré (dm²) ou le centimètre carré (cm²).
Comprendre ce qu’est un mètre carré permet de mieux visualiser l’aire d’un espace et de faire des calculs plus précis. Cela aide aussi à comparer des surfaces entre elles, à estimer des travaux ou à comprendre les plans et les cartes.
Des formules pour calculer certaines aires
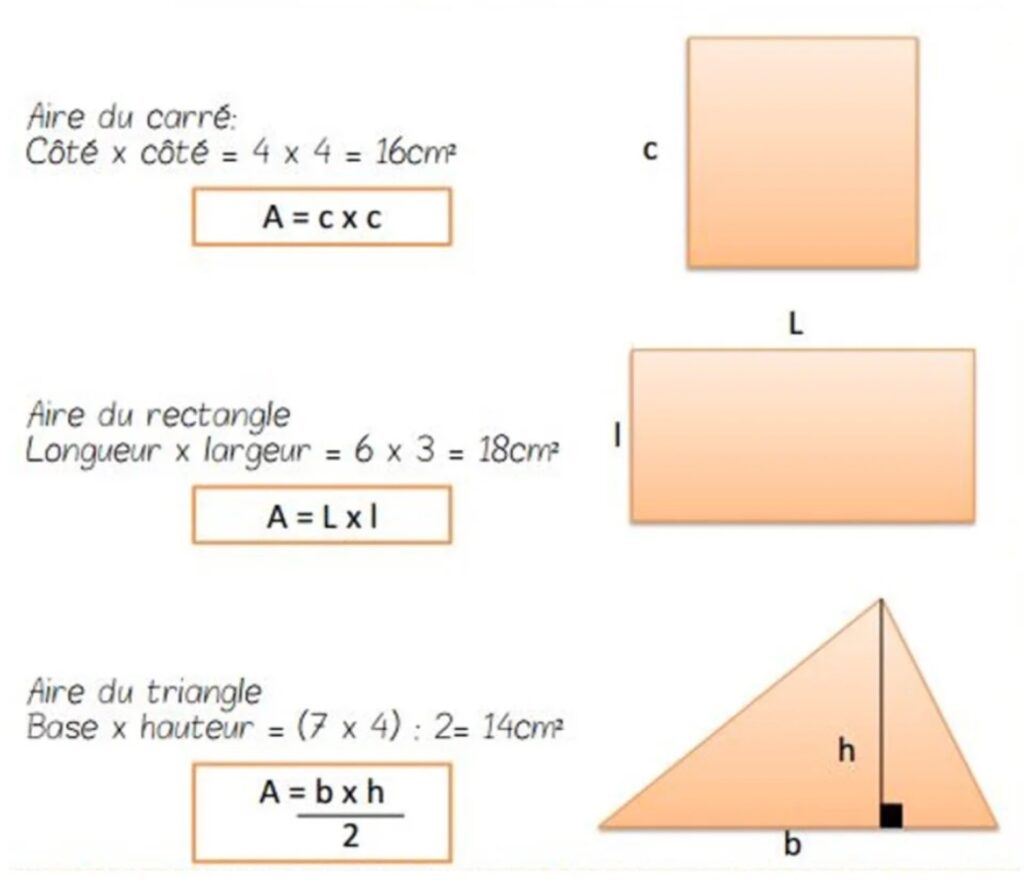
On peut calculer l’aire du carré et l’aire du rectangle en CM2 en utilisant des formules. En 6ème, on pourra également utiliser une formule plus complexe pour calculer l’aire d’un triangle.
Aire du carré = Côté x Côté Aire du rectangle = Longueur x Largeur
Ne pas confonde Périmètres et Aires !
Lis correctement la consigne pour éviter de les confondre.
Formules à connaître Périmètres et Aires !
| Figure | Formule du périmètre | Formule de l’aire |
|---|---|---|
| Carré | Côté x 4 | Côté x Côté |
| Rectangle | ( 2 x Longueur ) + ( 2 x Largeur ) | Longueur x Largeur |
Quelles compétences sont travaillées pour les élèves de CM1 CM2 sur les aires ?
| Compétence sur les aires | Indicateur de réussite (ce que l’élève sait faire) | Lien programme / ressource officielle |
|---|---|---|
| Identifier l’aire d’une surface géométrique | L’élève sait que l’aire correspond à la surface couverte à l’intérieur d’une figure (et non à son contour) | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Calculer l’aire d’un polygone simple (carré, rectangle…) | L’élève applique correctement les formules d’aire selon les figures étudiées (ex : aire d’un rectangle = longueur × largeur) | SOS Cartables – « Les unités d’aire » (fiches + conversion) (sos-cartables.fr) |
| Estimer ou comparer des aires | L’élève compare deux surfaces selon leur aire, justifie ses choix (ex : « cette surface est plus grande que celle‐ci ») | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Résoudre des problèmes impliquant l’aire | L’élève choisit et utilise la bonne formule ou stratégie pour résoudre des situations de la vie courante (ex : combien de carreaux pour couvrir un sol) | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Relier l’aire à d’autres grandeurs (longueurs, périmètre…) | L’élève distingue clairement l’aire d’autres notions (ex : périmètre = contour, aire = surface) et peut l’expliquer | Programme cycle 3 – Mathématiques (BO 17 avril 2025) – Eduscol |
| Utiliser les unités d’aire et leur conversion | L’élève utilise correctement les unités d’aire (cm², m²…) et peut effectuer des conversions simples | SOS Cartables – « Les unités d’aire » (sos-cartables.fr) |
Histoire des aires
L’aire d’une figure, c’est la mesure de la surface qu’elle occupe. Pour la trouver, on calcule combien d’espace est couvert à l’intérieur des contours. Par exemple, si on veut connaître l’aire d’un rectangle de 5 cm de long et 3 cm de large, on fait 5 × 3 = 15 cm². L’aire sert à savoir quelle surface doit être peinte, recouverte, carrelée ou coloriée. Elle s’exprime toujours dans une unité de surface : centimètre carré, mètre carré, etc. Plus la figure est grande, plus l’unité utilisée doit être adaptée.
La notion d’aire est très ancienne elle aussi. Les Égyptiens et les Babyloniens mesuraient déjà des surfaces pour partager des terres, calculer la récolte ou construire des bâtiments. Le mot « aire » vient du latin « area », qui signifiait une surface plane, un espace dégagé. Depuis longtemps, les êtres humains ont donc eu besoin de mesurer des surfaces pour organiser leur vie et leur territoire. Aujourd’hui, l’aire s’applique à toutes sortes de formes : carrés, rectangles, triangles ou surfaces plus complexes. Comprendre comment la calculer aide à mieux comprendre l’espace et la géométrie qui nous entourent.
Dans la vie quotidienne, nous utilisons l’aire sans toujours y penser. Quand on veut savoir combien de peinture il faut pour un mur, combien de carreaux pour une salle de bain ou quelle surface de gazon acheter pour un jardin, on calcule une aire. On multiplie ou on utilise des formules adaptées pour obtenir la surface totale. Savoir mesurer une aire permet de résoudre de nombreux problèmes concrets et d’observer plus précisément notre environnement. Cette compétence est utile pour les travaux, les projets d’école, les constructions ou même certains jeux où l’on doit comparer des surfaces.