Nous travaillons aujourd’hui le repérage des nombres décimaux sur des droites graduées. Tu peux retrouver la leçon ici pour en savoir plus ! –> (leçon ici)
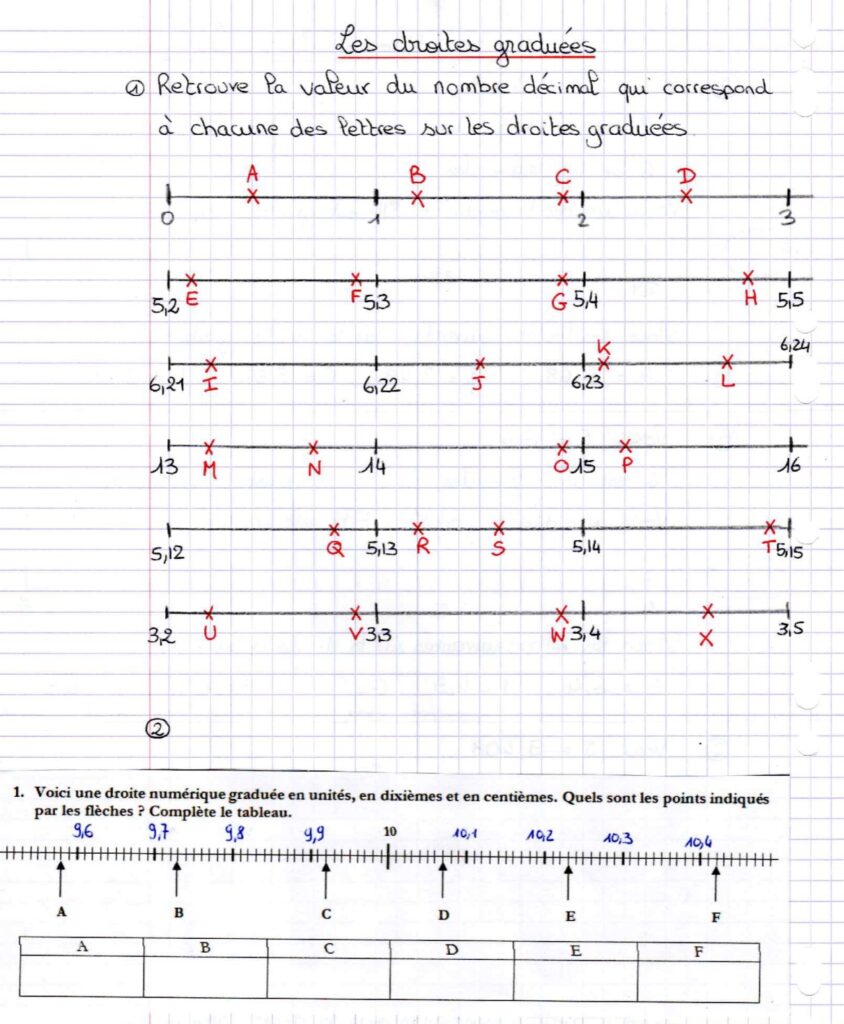
Correction des exercices : nombres décimaux et droites graduées

Explications des exercices sur les droites gradés et les nombres décimaux : partie 1
A : Dans un premier temps, nous analysons la droite graduée. Pour aller de 0 jusqu’à 1 unité, il y a 10 petites graduations. Une unité est donc découpée en 10 par conséquent nous avançons de dixième en dixième. Sur la droite graduée, on transforme tous les nombres afin d’avoir un chiffre après la virgule. Cela permet de trouver 0,0 au lieu de 0 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
B : Dans un second temps, nous analysons la droite graduée. Pour aller de 5,2 jusqu’à 5,3, il y a 10 petites graduations. Un dixième est donc découpée en 10 par conséquent nous avançons de centième en centième. Sur la droite graduée, on transforme tous les nombres afin d’avoir 2 chiffres après la virgule. Cela permet de trouver 5,20 au lieu de 5,2 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
C : Dans un troisième temps, nous analysons la droite graduée. Pour aller de 6,21 jusqu’à 6,21, il y a 10 petites graduations. Un centième est donc découpée en 10 par conséquent nous avançons de millième en millième. Sur la droite graduée, on transforme tous les nombres afin d’avoir 3 chiffres après la virgule. Cela permet de trouver 6,210 au lieu de 6,21 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
Explications des exercices sur les droites gradés et les nombres décimaux : partie 2
D : Dans un quatrième temps, nous analysons la droite graduée. Pour aller de 13 jusqu’à 14 unités, il y a 10 petites graduations. Une unité est donc découpée en 10 par conséquent nous avançons de dixième en dixième. Sur la droite graduée, on transforme tous les nombres afin d’avoir un chiffre après la virgule. Cela permet de trouver 13,0 au lieu de 13 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
E : Dans un cinquième temps, nous analysons la droite graduée. Pour aller de 5,12 jusqu’à 5,13, il y a 10 petites graduations. Un centième est donc découpée en 10 par conséquent nous avançons de millième en millième. Sur la droite graduée, on transforme tous les nombres afin d’avoir 3 chiffres après la virgule. Cela permet de trouver 5,120 au lieu de 5,12 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
F : Dans un sixième temps, nous analysons la droite graduée. Pour aller de 3,2 jusqu’à 3,3, il y a 10 petites graduations. Un dixième est donc découpée en 10 par conséquent nous avançons de centième en centième. Sur la droite graduée, on transforme tous les nombres afin d’avoir 2 chiffres après la virgule. Cela permet de trouver 3,20 au lieu de 3,2 par exemple et de simplifier la tâche à effectuer. On peut alors donner la valeur de chaque lettre sur la droite graduée plus facilement.
Explications sur les exercices : partie 3
Pour terminer, nous savons que la droite est graduée en unité, en dixième et en centième. Sur la droite, apparaît le nombre 10 qui correspond aux unités. Chaque unité est décomposée en dixième et chaque dixième est décomposée en centième. Chaque petite graduation correspond donc à 1 centième. Enfin, chaque petite graduation foncée correspond donc à 1 dixième et chaque grande graduation correspond à une unité.



