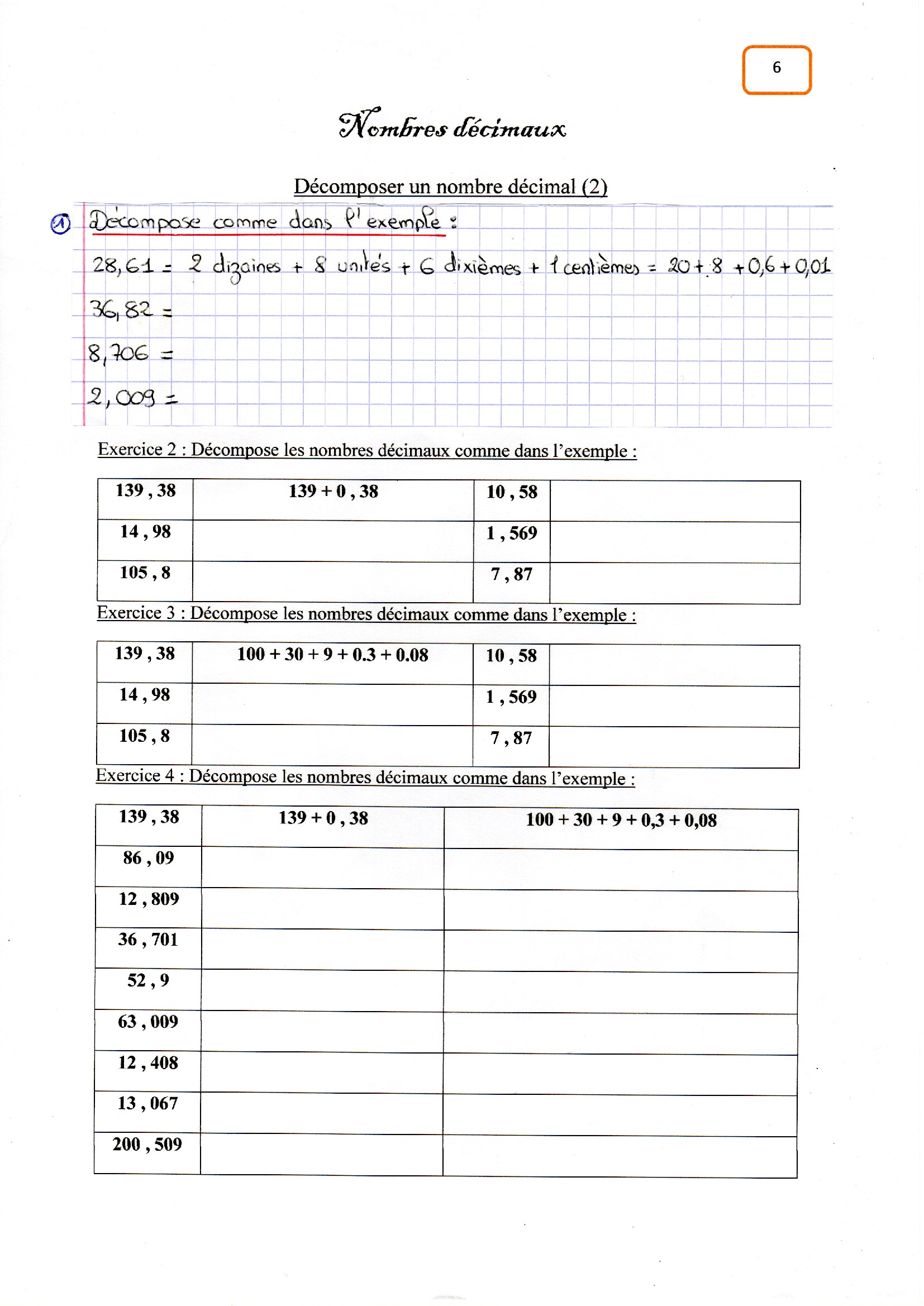
Exercices d’application sur la décomposition des nombres décimaux (voir leçon ici !)
Exercices d’application sur les nombres décimaux
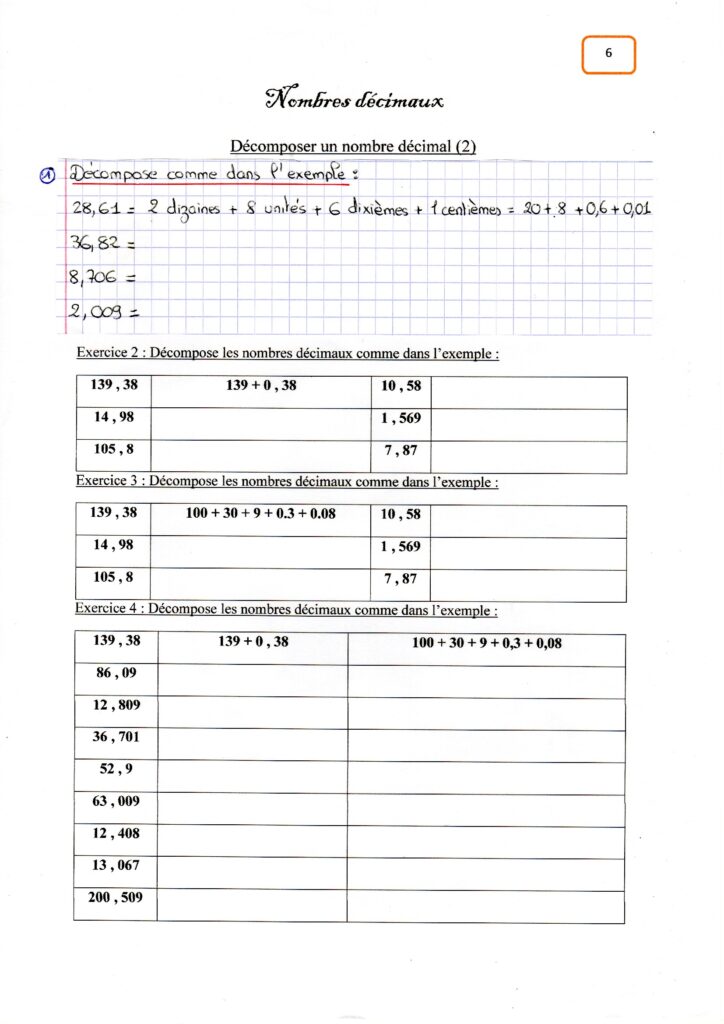
Correction des exercices d’application sur la décomposition des ND.
https://www.youtube.com/@soscartables
📌 Qu’est-ce qu’une décomposition additive ?
La décomposition additive d’un nombre décimal, c’est exprimer ce nombre comme une somme de plusieurs termes, en détaillant la valeur de chaque chiffre selon sa position dans le nombre.
On utilise le système de numération décimale :
- À gauche de la virgule ➔ des unités, dizaines, centaines…
- À droite de la virgule ➔ des dixièmes, centièmes, millièmes…
🏗️ Exemple de décomposition additive
Prenons le nombre :
125,307
On le décompose ainsi : 125,307=100+20+5+0,3+0,007‾125,307 = 100 + 20 + 5 + 0,3 + 0,00\underline{7}125,307=100+20+5+0,3+0,007
Pourquoi ?
- Le chiffre des centaines (1) vaut 100
- Le chiffre des dizaines (2) vaut 20
- Le chiffre des unités (5) vaut 5
- Le chiffre des dixièmes (3) vaut 0,3
- Le chiffre des centièmes (0) vaut 0 (on peut l’omettre)
- Le chiffre des millièmes (7) vaut 0,007
📌 Qu’est-ce qu’une décomposition multiplicative ?
La décomposition multiplicative, c’est une autre façon d’exprimer un nombre décimal :
✅ On écrit chaque chiffre multiplié par sa valeur de position.
✅ Cela aide à bien comprendre la valeur de chaque chiffre selon sa place dans le nombre.
🏗️ Exemple 1 : 125,307
Voici comment le décomposer multiplicativement :
125,307= (1×100)+(2×10)+(5×1)+(3×0,1)+(0×0,01)+(7×0,001)
🔎 Détail :
- 1 est dans la colonne des centaines, donc : 1 × 100
- 2 est dans la colonne des dizaines, donc : 2 × 10
- 5 est dans la colonne des unités, donc : 5 × 1
- 3 est dans la colonne des dixièmes, donc : 3 × 0,1
- 0 est dans la colonne des centièmes, donc : 0 × 0,01 (souvent on ne l’écrit pas)
- 7 est dans la colonne des millièmes, donc : 7 × 0,001