Voici la leçon sur les soustractions de nombres entiers et les additions décimales . Tu pourras retrouver la leçon précédente ici ! Clique ici pour revenir sur la page d’accueil !
CP3 : Les soustractions (nombres entiers)
Le sens de la soustraction
La soustraction permet de :
- calculer ce qui reste, ce qu’on a enlevé dans une collection.
- calculer un écart entre 2 choses (distances, prix…)
- reculer sur la file numérique
Quand on effectue une soustraction, on calcule une différence.
Technique de la soustraction
Il faut toujours aligner les unités avec les unités, les dizaines avec les dizaines… On ne peut mettre qu’un chiffre par colonne.
Soustraction sans retenue

1- D’abord, on pose la soustraction correctement ! On écrit les unités en premier. Il n’y a qu’un chiffre par carreau !
2- On commence le calcul par les unités : 5 – 4 = 1. On pose 1.
3- On continue avec les dizaines : 6 – 2 = 4 On pose 4.
4- On finit avec les centaines : 8 – 0 = 8. On pose 8.
La différence est égale à 841.
Soustraction avec retenue

1- D’abord, on pose la soustraction correctement ! On écrit les unités en premier. Il n’y a qu’un chiffre par carreau !
2- On commence le calcul par les unités : 2 – 9 Impossible. On ajoute donc 10 unités (1 dizaine) à 2, on a donc 12 unités.
3- On ajoute aussi 1 dizaine à 3 pour équilibrer, on a donc 4 dizaines 12 – 9 = 3 On pose 3.
4- On continue avec les dizaines : 9 – 4 = 5 On pose 5.
5- On finit avec les centaines : 5 – 2 = 3 On pose 3.
La différence est égale à 353.
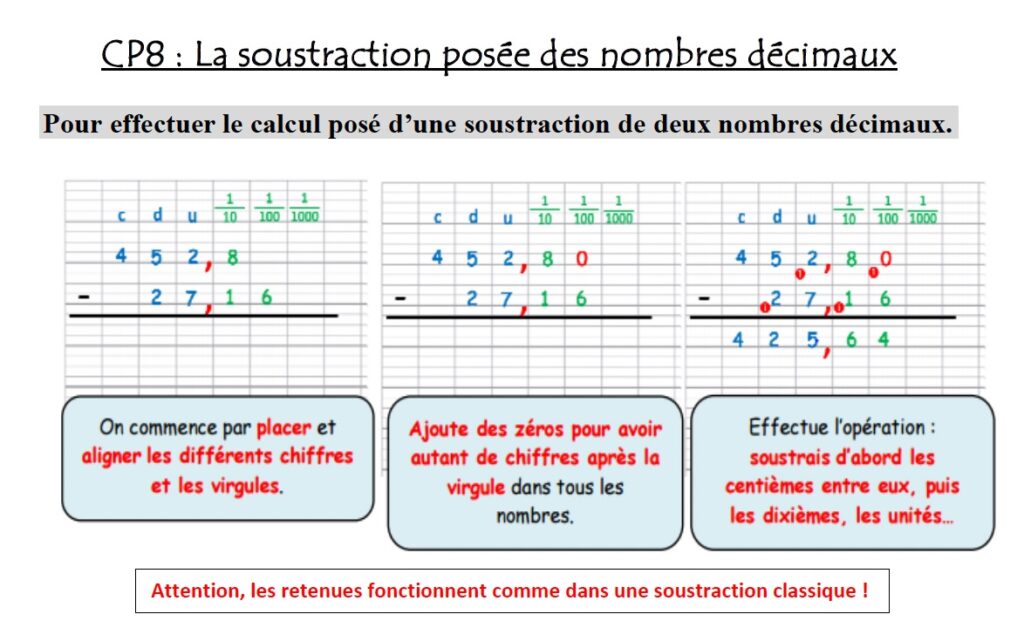
CP8 : Les soustractions décimales
Les compétences à travailler sur les soustractions
| Compétence | Indicateur de réussite |
|---|---|
| Comprendre le sens de la soustraction | L’élève sait que la soustraction sert à retirer, comparer des quantités ou calculer un écart |
| Poser et effectuer une soustraction d’entiers | L’élève aligne correctement les chiffres selon les unités, dizaines, centaines… et effectue la soustraction sans erreur |
| Utiliser des stratégies de calcul mental | L’élève soustrait mentalement des entiers simples en utilisant des décompositions connues (dizaines, compléments à 10…) |
| Vérifier la cohérence d’un résultat | L’élève estime le résultat attendu et repère une erreur éventuelle dans son calcul |
| Résoudre des problèmes mettant en jeu des soustractions | L’élève choisit la soustraction comme opération adaptée à la situation et justifie son choix |
| Compétence sur les soustractions | Indicateur de réussite : les soustractions |
|---|---|
| Comprendre la valeur des chiffres dans un nombre décimal | L’élève identifie la partie entière et la partie décimale, et sait lire un nombre décimal correctement |
| Poser et effectuer une soustraction de nombres décimaux | L’élève aligne correctement les chiffres selon la virgule et effectue le calcul sans erreur |
| Utiliser des stratégies de calcul mental avec les décimaux | L’élève soustrait mentalement des nombres décimaux simples (ex : 4,7 − 2,3) en s’appuyant sur les entiers correspondants |
| Vérifier la cohérence d’un résultat | L’élève estime le résultat attendu en s’appuyant sur un ordre de grandeur |
| Résoudre des problèmes impliquant des soustractions de décimaux | L’élève choisit la soustraction adaptée à une situation (prix, longueurs, mesures…) et explique sa démarche |
https://www.youtube.com/@soscartables
Histoire des soustractions !
La soustraction est une opération aussi ancienne que l’addition. Déjà les Égyptiens, les Babyloniens et les Grecs l’utilisaient pour comparer des quantités, retirer des portions et savoir ce qui restait après avoir pris une partie d’un total. Même si leurs chiffres étaient différents des nôtres, le principe de “retirer pour trouver le reste” était le même.
Avec l’invention du zéro et du système décimal par les savants indiens, les calculs sont devenus beaucoup plus simples et précis, y compris pour les soustractions. La méthode de poser une soustraction, en alignant les nombres selon les unités, dizaines et centaines pour calculer colonne par colonne, a été développée par les mathématiciens indiens et arabes.
Cette technique est arrivée en Europe grâce à Fibonacci au XIIIᵉ siècle. Aujourd’hui, elle est enseignée à l’école et reste indispensable pour résoudre des problèmes du quotidien, comparer des quantités et calculer des écarts avec précision.



Ping : La multiplication : leçon CM1-CM2
Ping : La multiplication : leçon CM1-CM2
Ping : CP3 Le sens de la soustractions : approche et explications