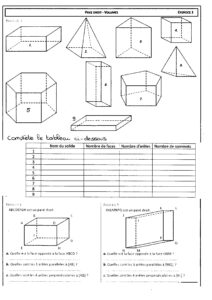
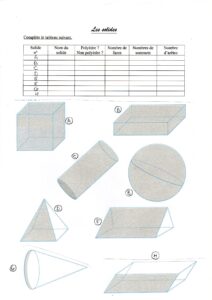
Fiche d’exercice n°5 sur les solides
Retrouve la leçon sur les solides ici ! Dans cette fiche d’exercices n°6 sur les solides, nous allons caractérisé ceux-ci en fonction du nombre de faces, du nombre d’arêtes et du nombre de sommets.
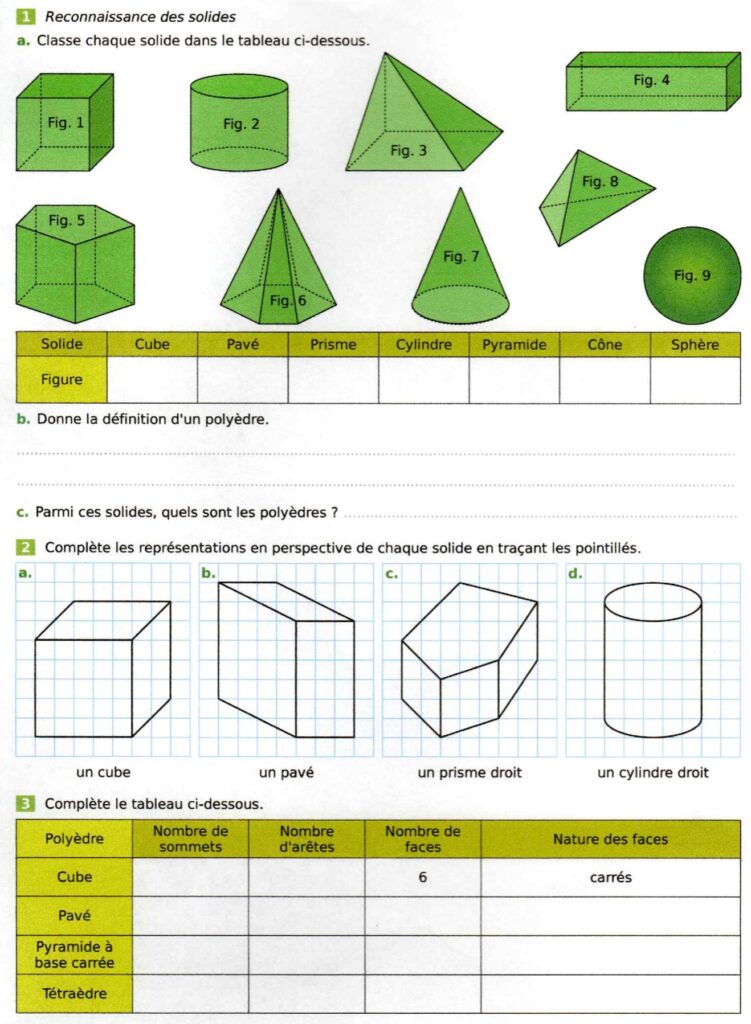
Fiche corrigée sur les solides
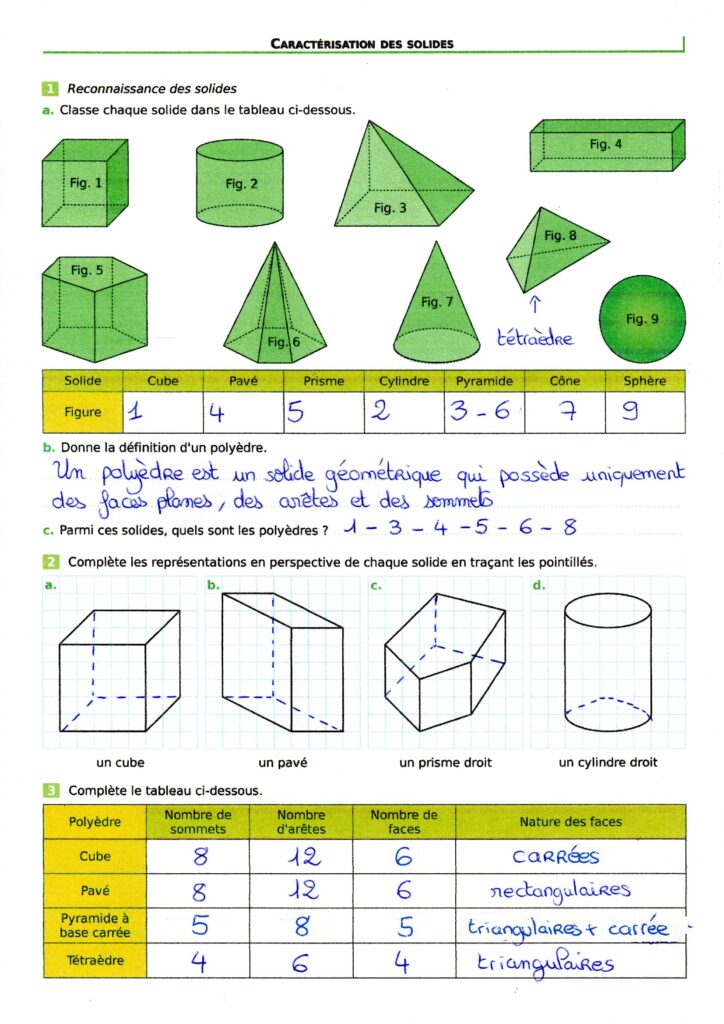
Un solide est un objet qui occupe un volume. Il a :
✅ des faces (les surfaces plates ou courbes),
✅ des arêtes (les côtés),
✅ des sommets (les coins).

Vocabulaire à connaître pour sa leçon sur les solides!
Face : une surface plane (ou courbe) qui forme un côté du solide.
Arête : un côté, c’est la ligne qui relie deux faces.
Sommet : un coin, c’est l’endroit où plusieurs arêtes se rejoignent.
Un pavé droit (ou parallélépipède rectangle) a : 6 faces rectangulaires, 8 sommets et 12 arêtes.
Polyèdre ou non polyèdre ?
Un polyèdre est un solide géométrique qui possède uniquement des faces planes (polygones), des arêtes et des sommets : un cube, une pyramide, un prisme, un pavé (ou parallélépipède rectangle), un tétraèdre…
Un non-polyèdre est un solide qui comporte au moins une surface courbe.
Exemples : sphère, cylindre, cône.
https://www.youtube.com/@soscartables
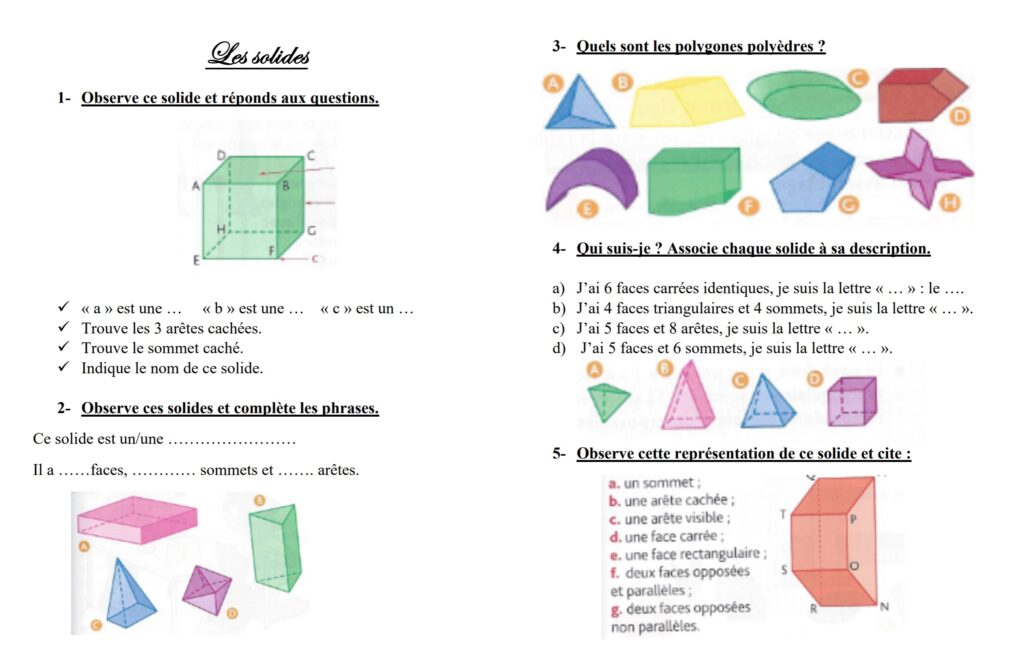
1- Face – arête – sommet – DH – HE – HG – H – ADCBEHGF
2- le premier solides est un pavé droit qui a six faces, huit sommets et 12 arêtes. Le second solides est un prisme qui a cinq faces, six sommets et neuf arêtes. Le solide suivant est une pyramide à base carrée qui a cinq faces, cinq sommets et huit arêtes. Pour terminer, le dernier solide est un prisme ayant huit faces, six sommets et 8 arêtes.
3- les polygones polyèdres sont : A – B – D – G – H
4- aD Cube – bA Tétraèdre – cC Pyramide à base carrée – dB Prisme
5- Multiples solutions
En savoir plus sur les tétraèdre !
Un tétraèdre est un solide géométrique qui a : 4 faces (toutes triangulaires), 4 sommets et 6 arêtes C’est le plus simple des polyèdres (solides à faces planes). Le mot vient du grec « tétra » (quatre) et « hedra » (face). Un tétraèdre régulier est un tétraèdre dont toutes les faces sont des triangles équilatéraux (mêmes côtés, mêmes angles). Il a 4 faces identiques, 6 arêtes de même longueur et 4 sommets équidistants. C’est un des 5 solides de Platon (solides parfaits et symétriques).